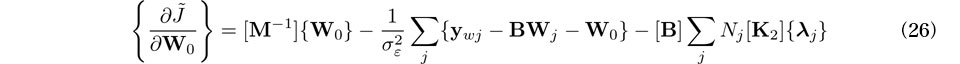1. レール軸力推定法の原理
左右レールは締結装置を介してまくらぎに接合されている.したがって,左右いずれか一方のレール作用力がわかっても道床横抵抗力を与えず,それらの合力を評価する必要がある.そのため,左右レール・まくらぎ連成系のつり合い状態について考える.
締結部における横作用力は,レールとまくらぎとの相対変位に依存する.すると,左右レールの水平たわみに関するつり合い式は次式で与えられる.
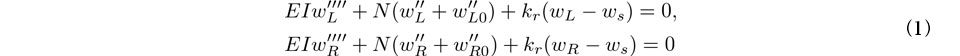
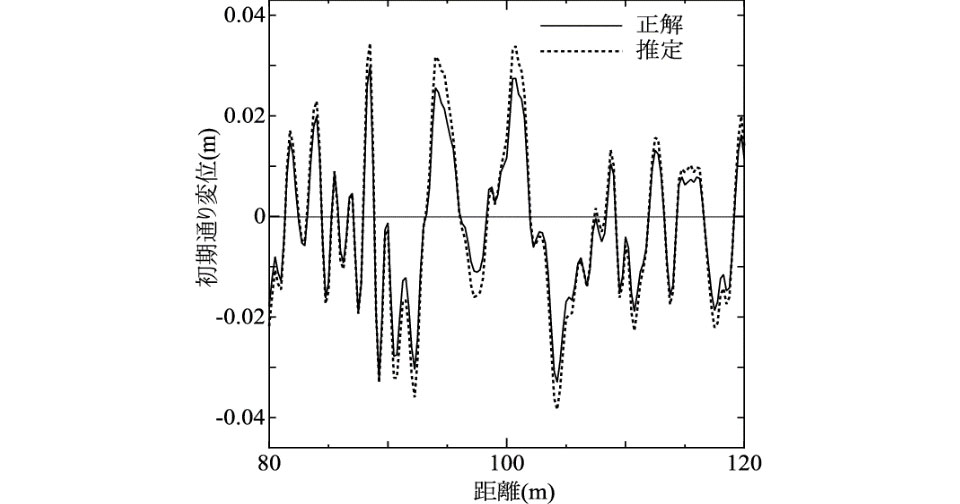
ここで,レールはEulerばりによりモデル化するものとし,Eはレールのヤング率,Iはレール弱軸回りの断面二次モーメント,Nは軸力(圧縮を正),wL, wRは左右レールの弾性たわみ,wL0, wR0はN=0における初期通り変位であり,( )'は軌道長手方向座標x に関する微分である.また,締結部のレール拘束力は本来離散的に作用するが,ここではそれを連続支持モデルにより近似表現している.なお,wsはまくらぎ横変位,krは締結部の横剛性(単位長さ当たり)である.本研究では,左右レール軸力は等しいものとする.また,「通り変位」はたわみ波形を意味する量として用いる.
道床横抵抗力がまくらぎ横変位に関して線形ばねksにより近似できるものと仮定すると,まくらぎのつり合い式は次式で与えられる.
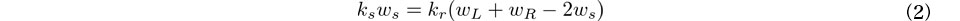
式(2)をwsについて解くと次式を得る.
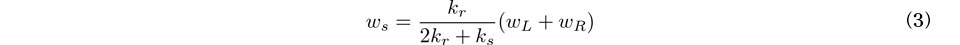
式(3)を式(1)に代入してwsを消去すると次式を得る.
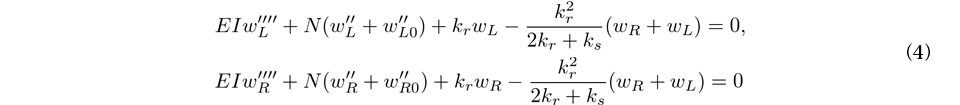
さらに式(4)両式の和をとると次式を得る.
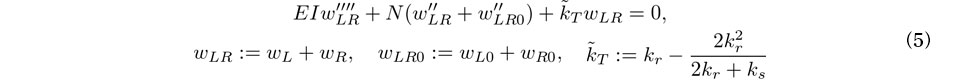
一方,軸力がN+ΔNであるときのつり合い式は,たわみ増分ΔwLRを用い次式により与えられる.
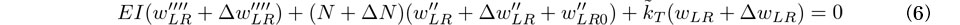
式(6)から式(5)第1式を引くと次式を得る.
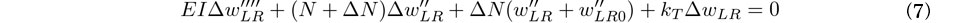
さらに式(7)のxに関するFourier変換より次式を得る.
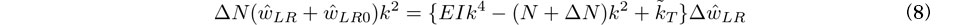
ここでkは波数,(^)はレール長手方向に関するFourier変換を意味する.
式(8)を整理して次式を得る.
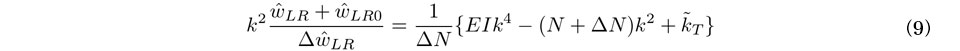
式(9)左辺は,通り変位の測定データとその差分をFourier変換することで求めることができる.式(9)右辺より,これは次のように波数kの4次関数で与えられる.
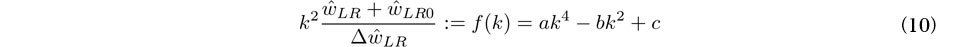
なお,以下では10m弦正矢ではなく,通り変位源波形データを対象として定式化を進める.
式(10)右辺の4次関数と,その係数a,b,c,および極小値を与える波数kmとの関係は,概略図1に示す様になる.なお,波数kmと絶対軸力N+ΔN,未知係数a,bらの関係は次式で与えられる.
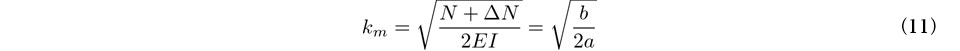
式(9), (10)および(11)より次式を得る.
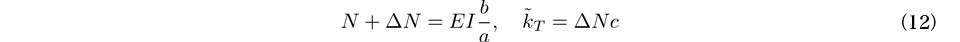
以上より,通り変位データのFourier変換より未知係数a,b,cを最小二乗法等により決定し,kmを求めれば,軸力N+ΔN(同様にN)および軌道横剛性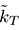 を推定することができる.
を推定することができる.
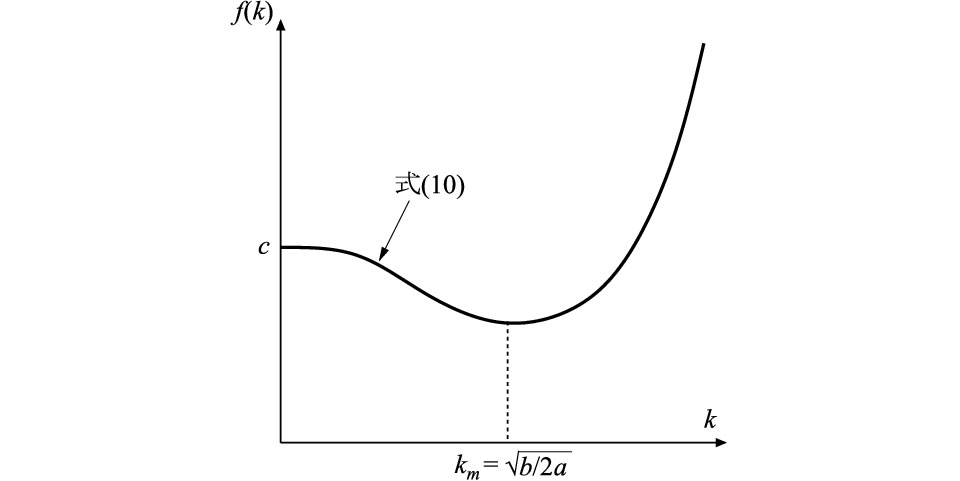
図1 式(9)の4次関数とその最小値を与える波数km
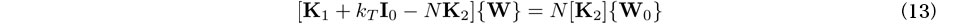
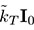 は,
は,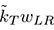 の項を離散化して得られる行列である.
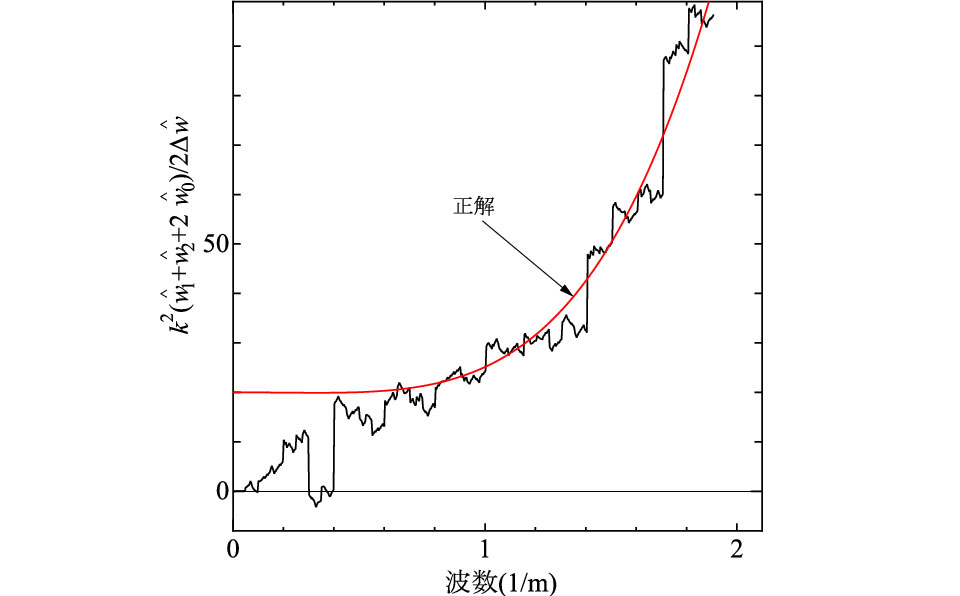
の項を離散化して得られる行列である.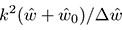 を求めた一例を図2に示す.なお,図には式(9)右辺の理論曲線を実線で示した.数値実験結果には長波長成分に乱れが認められるが,
を求めた一例を図2に示す.なお,図には式(9)右辺の理論曲線を実線で示した.数値実験結果には長波長成分に乱れが認められるが,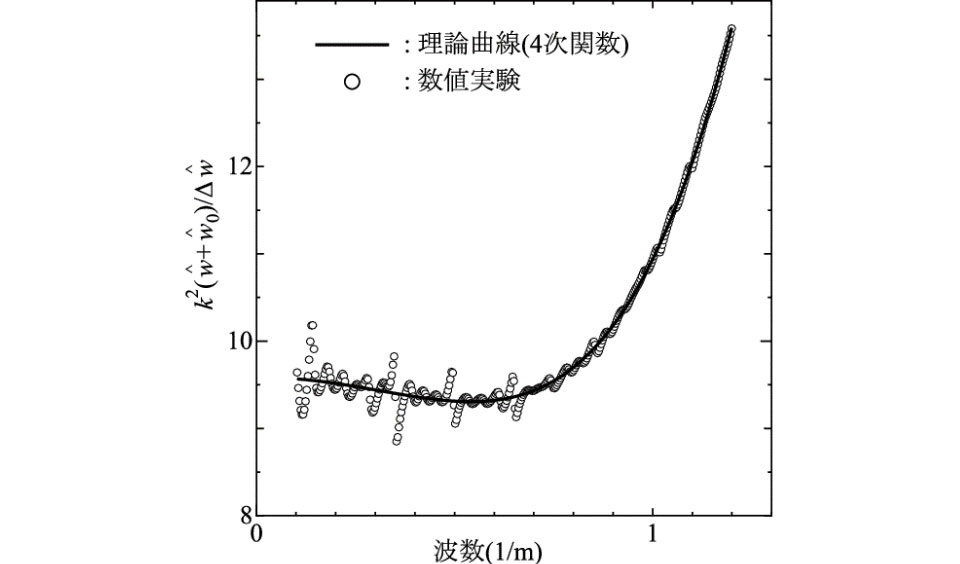
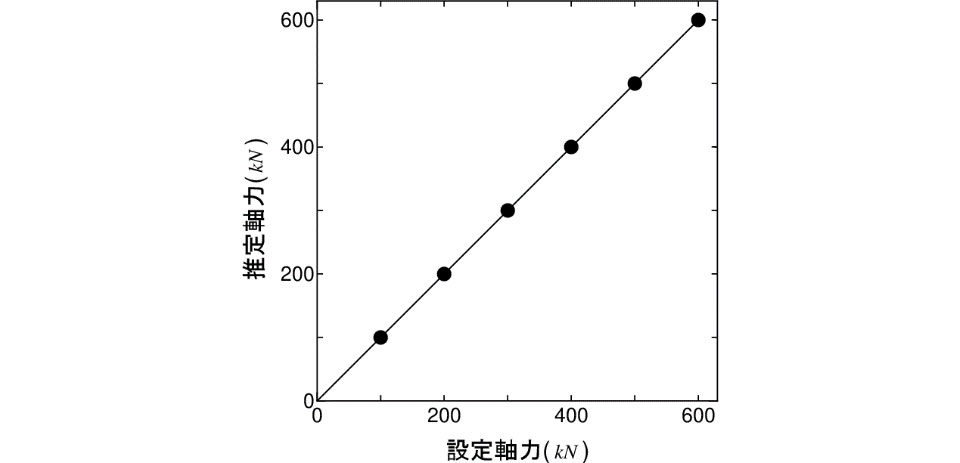
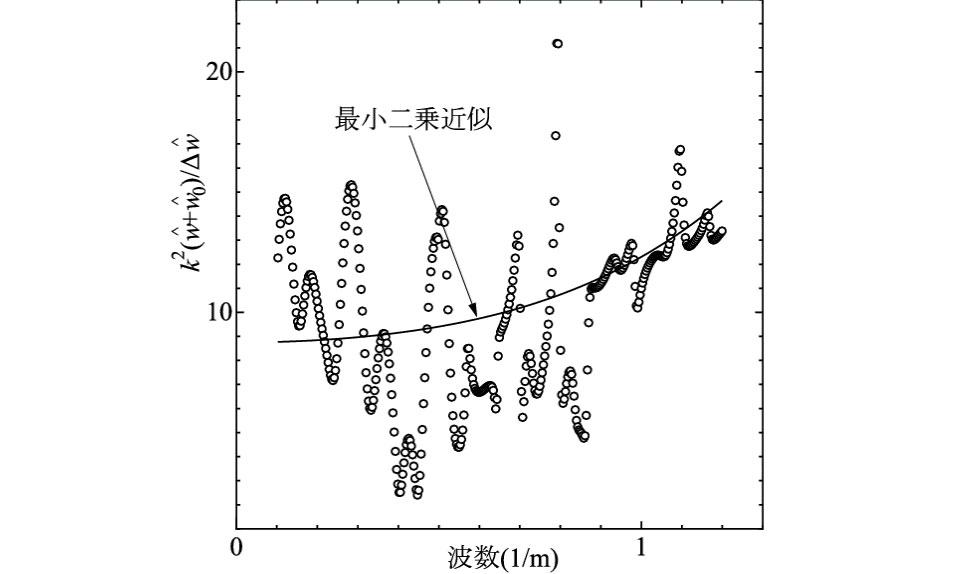
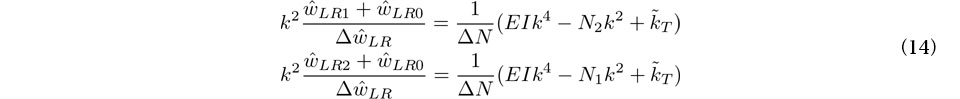
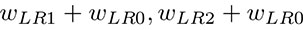 を計測量としている.よって,この2つのデータを同等に活用する目的で,軸力推定に用いる式を,式(14)両式の総和平均より得られる次式に修正する.
を計測量としている.よって,この2つのデータを同等に活用する目的で,軸力推定に用いる式を,式(14)両式の総和平均より得られる次式に修正する.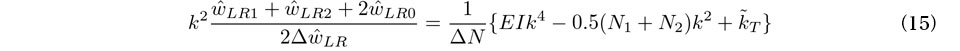
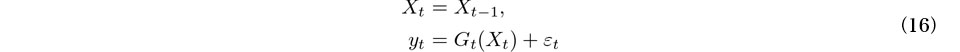
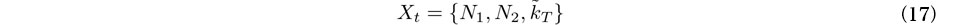
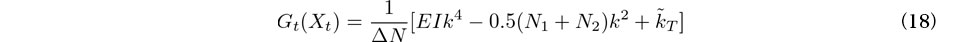
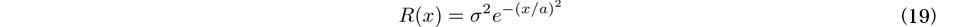
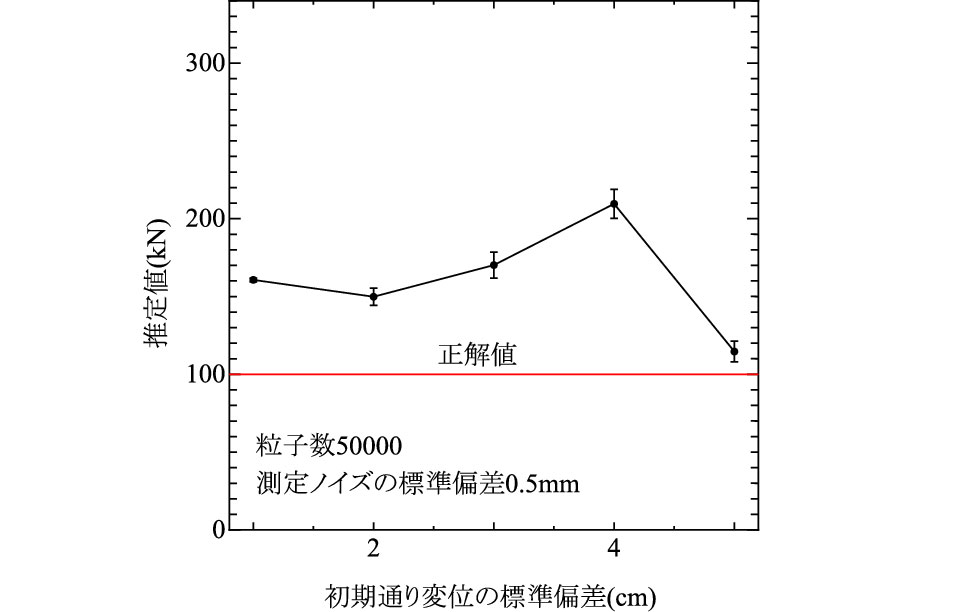
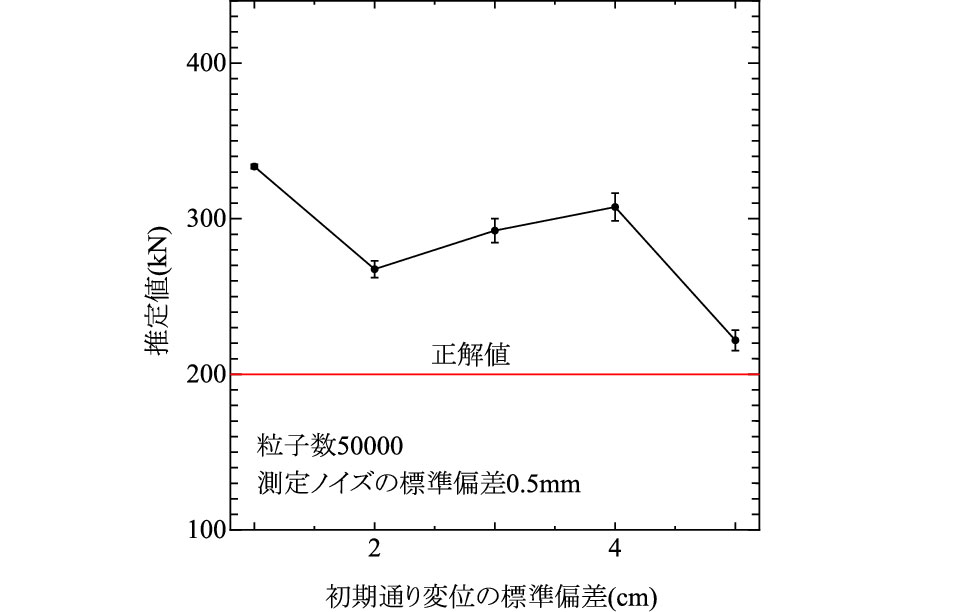
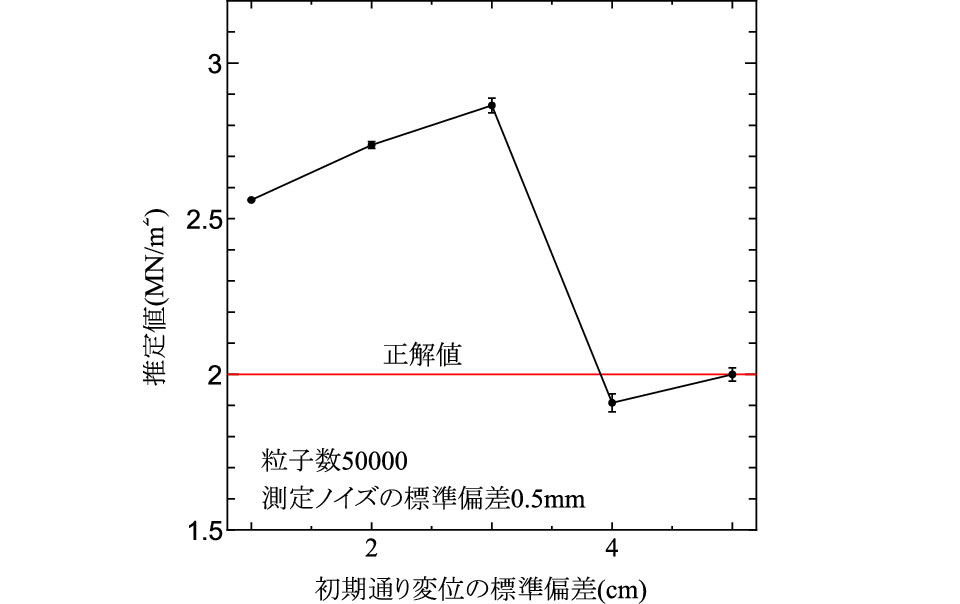
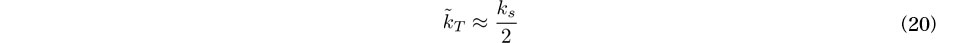
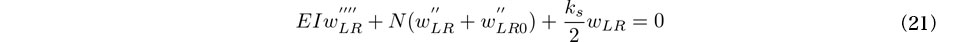
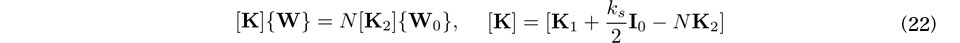
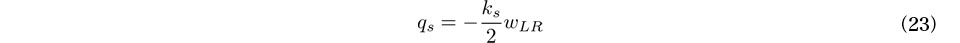
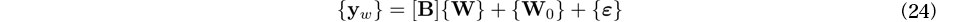
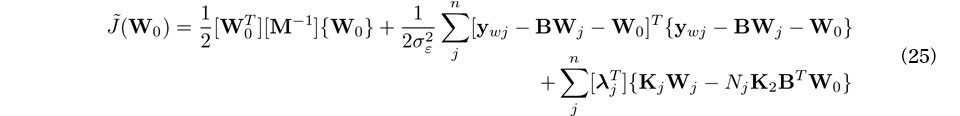
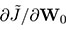 は次式で評価できる.
は次式で評価できる.