国内外の鉄道の多くには，列車荷重の分散・衝撃力の作用の緩和・振動低減を目的として，レールとまくらぎの下にバラスト道床として25cm程度の層厚で砕石を敷設します．バラスト道床には，非常に多数回の列車通過の結果，道床部には残留変位が生じ，特に道床上面における鉛直方向の残留変位は「道床沈下」と呼ばれています．本研究室では，バラスト道床部全体を弾塑性連続体としてモデル化し，有限要素法を用いて道床沈下量を定量的に効率よく予測する手法の開発に取り組んでいます． 道床沈下解析において弾塑性有限要素法の適用が可能になれば，バラスト道床の形状モデルの作成が容易になるだけでなく， 個別要素法（DEM）などの不連続性体解析手法を適用する場合と比べて，沈下解析の計算コストを大幅に軽減することが可能となります．

　Cyclic densificationモデル[1]は，弾塑性モデルの一種で，繰り返し載荷時の計算負荷を軽減することを目的に，Suikerらが提唱した構成モデルです． 単位サイクル数当たりの応力やひずみ，内部状態変数の変化量を直接定量化する形（繰り返し載荷モデル）で定義することから， それらをサイクル数について積分することで，繰り返し載荷での最大荷重作用時のつり合い状態における物体内の物理量の変化を効率よく追跡することができます． なお，解析に適用する際には，無荷重時と最大荷重作用時との間の単調載荷・除荷過程におけるつり合い状態を追跡・評価する必要があり， 単調載荷・除荷過程における弾塑性挙動を表現するための古典的弾塑性論に基づく構成モデル（単調載荷モデル）と組み合わせて使用する必要があります．
　単調載荷モデルでは，圧力依存性を有する亜弾性構成則を出発点として，引張破壊と圧壊を表現する降伏曲面を有する修正 Drucker-Pragerモデル（図 1(a)参照）を導入し， 摩擦性材料の弾塑性解析で広く行われているように，非関連流動則を適用することとします． 一方，繰り返し載荷モデルでは，単調載荷モデルと同様に圧力依存性を有する亜弾性挙動を仮定し，塑性流動則として非関連流動則を適用しますが， ただし，超過応力モデルにおいて塑性流動の閾値であるシェイクダウン応力は，単調載荷モデルの降伏関数と同様に， 修正 Drucker-Prager型の円錐面と2平面の組み合わせ（図 1(b)参照）により与えます．
 

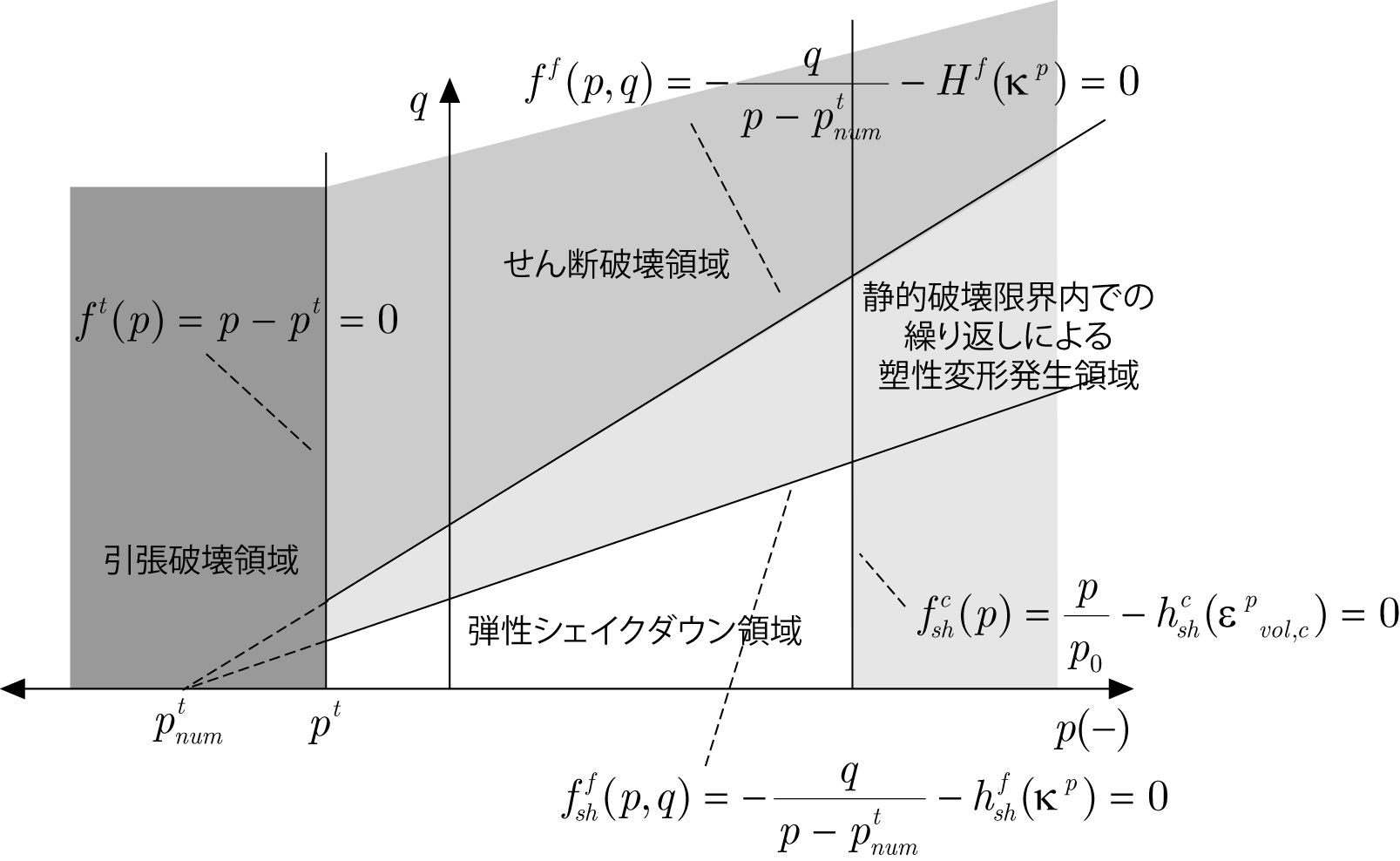(a) 単調載荷モデルの降伏曲面	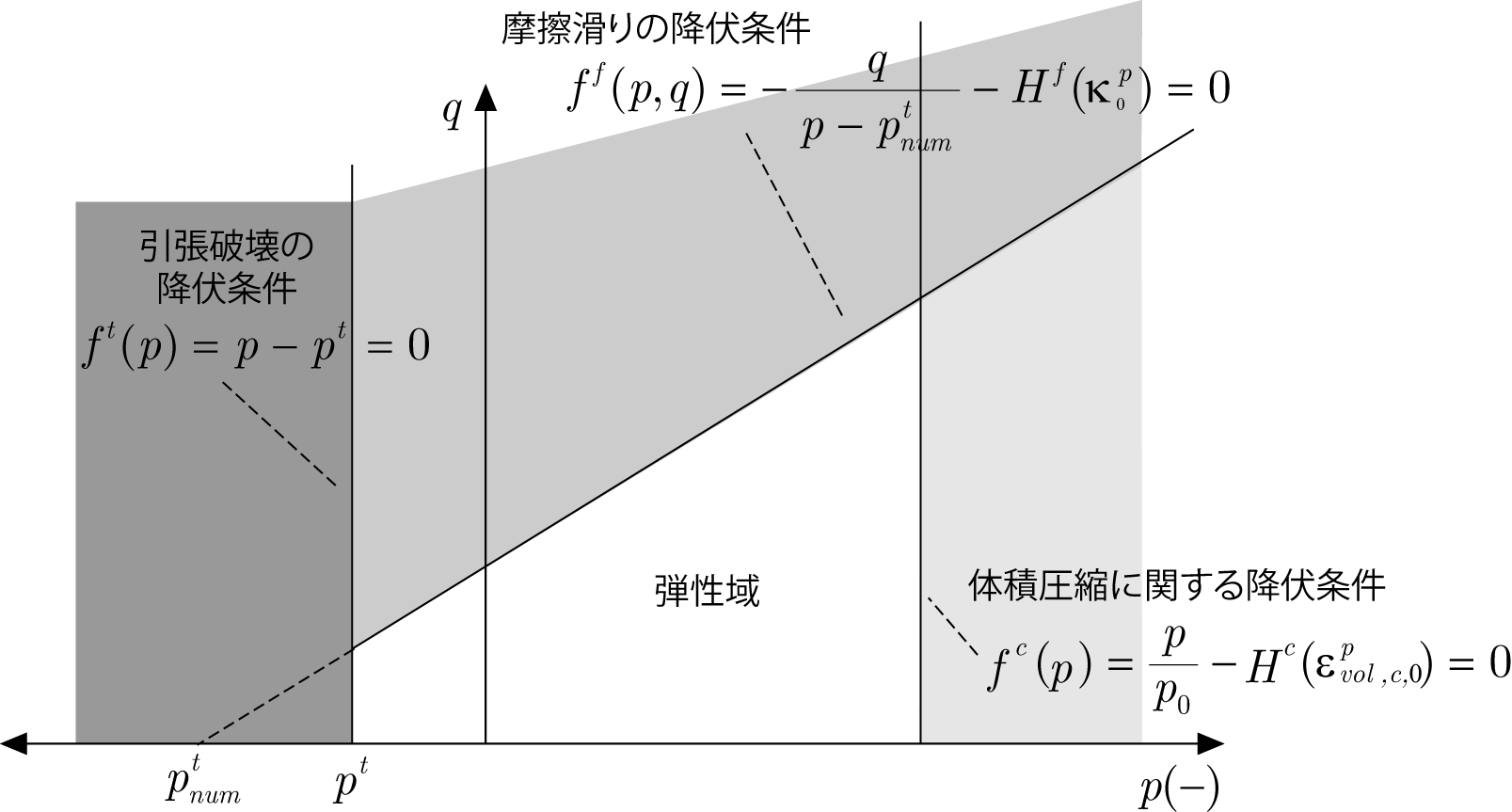(b) 繰り返し載荷モデルの破壊面
図 1 Cyclic densificationモデルにおける降伏曲面と破壊面

　本モデルのバラスト道床沈下解析への適用可能性を検討するために，石川らによる実物大軌道の繰り返し鉛直載荷試験[2]を模擬した解析条件の下で有限要素解析を行ないます． 図 2に示すようなバラストとまくらぎからなる解析領域を3次元有限要素モデルで表現し， レールの位置に鉛直方向の荷重（最大鉛直荷重を$P$=20kN）を繰り返し作用させた時の沈下量を評価してみます． 境界条件は，軌道縦断面および横断面に対称条件，バラスト道床底面には完全拘束条件をそれぞれ課し，バラストとまくらぎの間では接触・摩擦は考慮せず完全付着と仮定します．
 

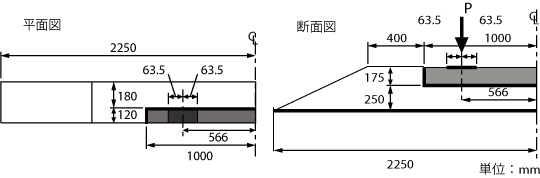図 2 解析領域および境界条件

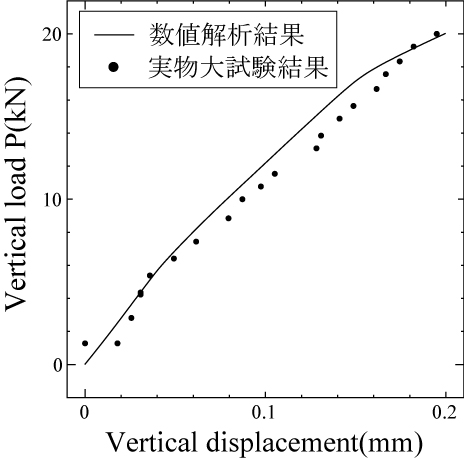
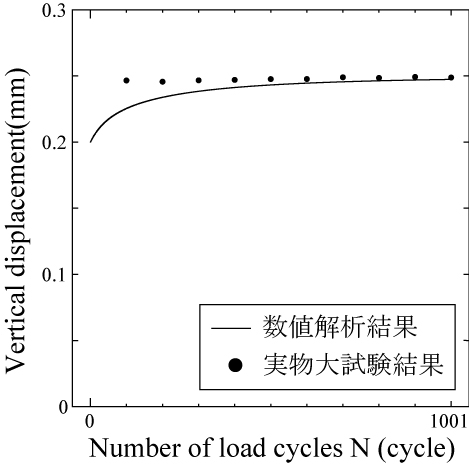(a) 鉛直荷重-鉛直変位関係の比較($P$=20kN)．　　 (b) 繰り返し載荷回数-鉛直変位関係の比較($P$=20kN)．

図 3 単調載荷過程・繰り返し載荷過程における解析結果と実験結果との比較

　ここで，図 3(a)に繰り返し載荷1回目におけるレール位置での鉛直変位と鉛直荷重との関係を， 図 3(b)は，最大鉛直荷重作用下でのレール位置における鉛直変位と繰り返し載荷回数との関係をそれぞれ示す．載荷初期では実験結果と解析結果との間に差があるものの， 繰り返し載荷回数を増すことで両者は同等の鉛直変位量に漸近しており，道床沈下挙動が定性的に矛盾なく再現できています．
　次に，弾塑性有限要素解析の計算負荷の軽減を図る目的で，平面ひずみ近似の妥当性について検討してみます． ここでは，図 4に示すような軌道横断方向の2次元平面ひずみ解析を考えます．平面ひずみ解析，3次元解析でそれぞれ得られた縦断面内の平均応力，偏差応力の２次不変量，塑性体積ひずみ，塑性偏差ひずみの２次不変量の分布を図 5に示します．

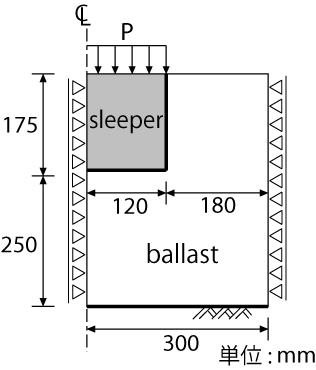図 4 軌道横断方向の平面ひずみ解析における境界条件

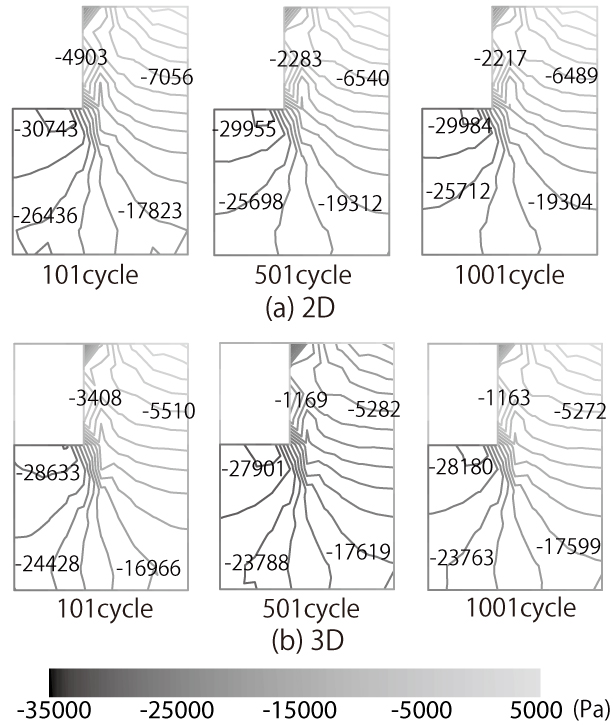
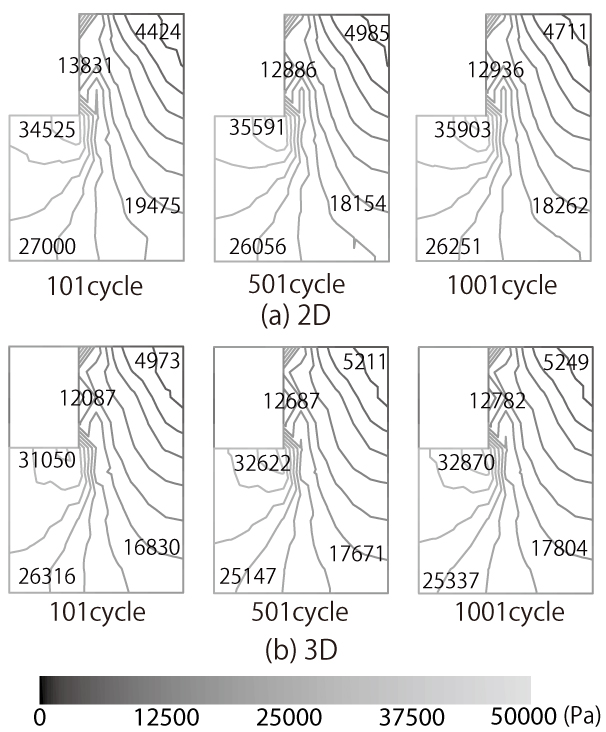(a) 平均応力　　　　　　　　　　　　　　　　 (b) 偏差応力の２次不変量

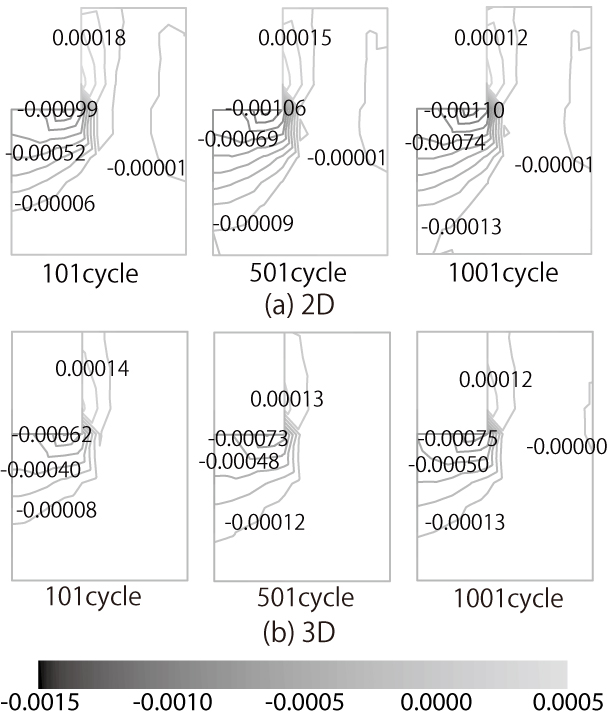
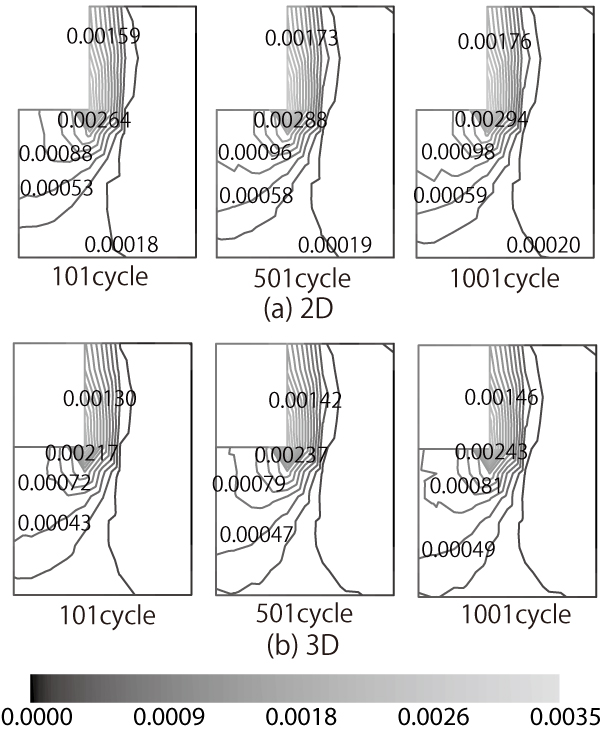(c) 塑性体積ひずみ　　　　　　　　　　　　　 (d) 塑性偏差ひずみの２次不変量

図 5 応力・塑性ひずみ不変量における2次元・3次元解析結果の比較

　軌道横断方向の平面ひずみ解析と３次元解析の応力・塑性ひずみを比較すると，ほぼ同様の分布となることがわかります． これは，まくらぎの剛性がバラストの剛性より高いために，鉛直荷重作用時にまくらぎの剛体的な移動によるバラストの圧縮変形が卓越するため，平面ひずみ近似が概ね成立していることが原因であると考えられます．
　最後に，3次元解析および軌道横断方向の平面ひずみ解析で得られた荷重作用位置における鉛直変位を図 6に示します． 平面ひずみ解析では3次元解析よりも変位が10\%程度大きく生じていますが，応力および塑性ひずみが大きめの値で評価されていることと矛盾がなく，安全側に評価されることが確認できます．

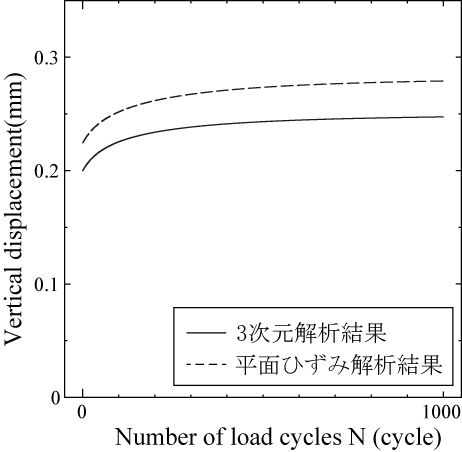図 6 平面ひずみ解析・3次元解析における鉛直変位

　なお，本節で示した研究成果は，文献[3]として公表しています．

　Cyclic densificationモデルを用いた道床沈下解析では，構成モデルとして「単調載荷モデル」と「繰り返し載荷モデル」の2種類を用い，それらのモデルにおいて用いられる材料パラメータは，実験結果から容易に決定できるものとそうでないものとが混在しています．そこで，発見的知識による最適化アルゴリズムの枠組みであるメタヒューリスティックスの一つである粒子群最適化（particle swarm optimization; PSO）[4]を用いて，解析に用いる材料パラメータの同定を試みています．
　PSOによるパラメータ同定においては，最小化を試みる目的関数を予め設定しておき，材料パラメータ群からなる有限サイズの個体群を準備します．各個体について目的関数値を計算し，個体毎の最良パラメータ群（パーソナルベスト），個体群全体での最良パラメータ群（グローバルベスト）を求めておき，これらの材料パラメータ群の近傍で材料パラメータ群の集合を繰り返し再生成・更新することで，材料パラメータの最適値の探索を効率よく行なうようにアルゴリズムが設計されています．
　上記手法を用いて，バラスト材の変形挙動を再現するような 材料パラメータ値の同定を試みます． 同定計算に際しては，同定計算を単調載荷過程と繰り返し載荷過程との2つに分離した上で，各々について Suikerらが示した大型三軸試験結果[5]を参照解に設定しました． 同定計算における目的関数 $J$は次式で与えました． \begin{equation} J=\omega_1\sum_{j=1}^{n_{mono}}|\kappa^{(j)}-\bar{\kappa}^{(j)}| +\omega_2\sum_{j=1}^{n_{mono}}|\varepsilon_{vol}^{(j)}-\bar{\varepsilon}_{vol}^{(j)}|, \hskip5mm （単調載荷過程） \nonumber \end{equation} \begin{equation} J=\omega_1\sum_{j=1}^{n_{cyc}}|d\kappa^{(j)}-d\bar{\kappa}^{(j)}| +\omega_2\sum_{j=1}^{n_{cyc}}|d\varepsilon_{vol}^{(j)}-d\bar{\varepsilon}_{vol}^{(j)}|, \hskip5mm （繰り返し載荷過程） \nonumber \end{equation} ここで，$\varepsilon_{vol}=\varepsilon_{kk}$として，$\kappa$は次式で定義することとし， \begin{equation} \kappa=\sqrt{\dfrac{2}{3}\gamma_{ij}\gamma_{ij}},\hskip5mm \gamma_{ij}=\varepsilon_{ij}-\dfrac{\varepsilon_{vol}}{3}\delta_{ij}, \nonumber \end{equation} $d\kappa$，$d\varepsilon_{vol}$は，第1サイクルでの $\kappa$，$\varepsilon_{vol}$の値 $\kappa_0$，$\varepsilon_{vol,0}$を基準として， \begin{equation} d\kappa=\kappa-\kappa_0,\hskip5mm d\varepsilon_{vol}=\varepsilon_{vol}-\varepsilon_{vol,0}, \nonumber \end{equation} と定義します．また，上付きの $\bar{\:}$は付された物理量の参照値であることを表わし，$n_{mono}$，$n_{cyc}$は，それぞれ単調載荷モデル・繰り返し載荷モデルの材料パラメータ同定に用いる参照値のデータ数，$\omega_1$，$\omega_2$は重み係数です．
　同定解析に際しては，まず，単調載荷モデルで用いる11個の材料パラメータ $K_{ref}$，$n^e$，$p_{ref}$，$\nu$，$P_0$，$H_0$，$H_m$，$\zeta^f$，$\zeta^c$，$D_0$，$D_m$のうち，$H_m$を除く10個を変数としました．単調載荷モデルの材料パラメータの同定解析後，繰り返し載荷挙動のみを参照解として，繰り返し載荷モデルの材料パラメータの同定解析を行ないました．繰り返し載荷モデルでのみ用いられる材料パラメータ $p_{0}$，$h_0$，$h_m$，$\eta^f$，$\eta^c$，$\alpha^f$，$\alpha^c$，$\gamma^f$，$\gamma^c$，$d_0$，$d_m$の11個のうち，$h_m$を除く10個を同定対象の変数としました．なお，$H_m=h_m=1.85$とし，個体数はいずれも30としました．
　材料パラメータ値を用いた順解析結果を図 7，図 8に示します．なお，順解析においては，最大主応力比 $(-q/p)_{max}=1.85$の下，繰り返し載荷解析で与える主応力比が $n=(-q/p)_{cyc}/ (-q/p)_{max}=0.964$となるように荷重を与えています． 載荷初期の参照解のデータ数が少なく，弾性挙動に関するパラメータ値の再現性はさほど高くないですが，塑性域での材料パラメータが参照解である実験結果を良好に再現する同定値であることが確認できます．
 

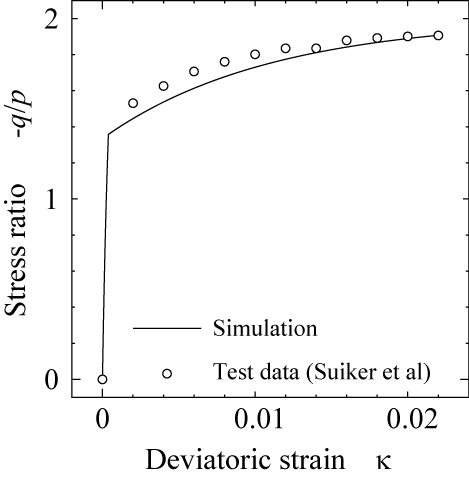
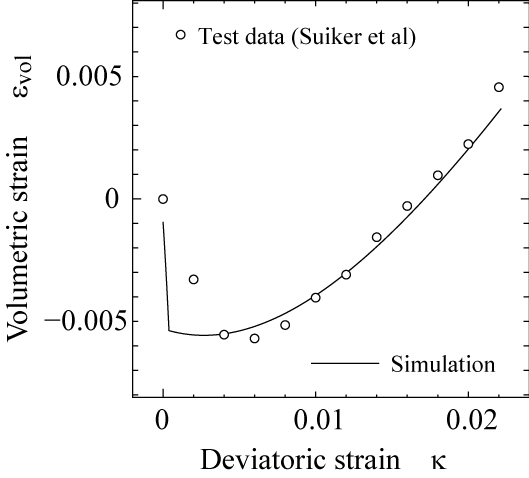(a) 主ひずみ $\kappa$と主応力比 $-q/p$ との関係．　　　　　　　　　 (b) 主ひずみ $\kappa$と体積ひずみ $\varepsilon_{vol}$ との関係．

図 7 同定した材料パラメータ値を用いた単調載荷解析結果（$\sigma_c=-41.3$kPa）．

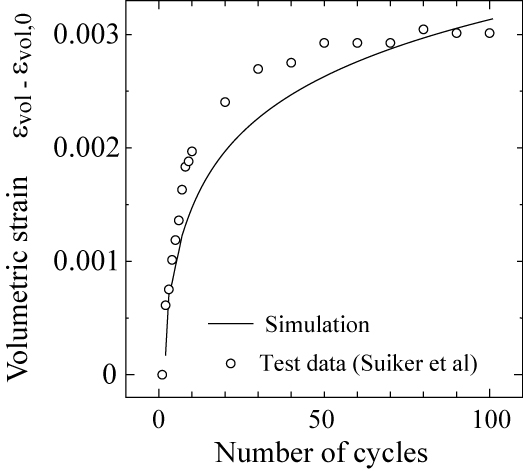(a) 繰り返し回数 $N$と相当ひずみ $\kappa-\kappa_0$ との関係． (b) 繰り返し回数 $N$と体積ひずみ $\varepsilon_{vol}-\varepsilon_{vol,0}$ との関係．

図 8 同定した材料パラメータ値を用いた繰り返し載荷解析結果（$\sigma_c=-41.3$kPa）．

　次に，同定した材料パラメータ値の下で，バラスト材の繰り返し変形解析結果に対する材料パラメータの影響感度を評価してみます．この影響感度は，当該モデルの材料パラメータ値の同定プロセスを考えると，（材料試験結果から観測される）バラスト材の力学挙動のばらつきが，繰り返し変形解析結果に伝播する影響の度合いを表わすものとみなすことができます．
　感度評価解析は，2次近似2次モーメント法(Second-Order Second-Moment method; SOSM)を用いて行ないます． SOSMでは，変動を考慮する材料パラメータを $\boldsymbol{p}=\{p_i|i=1,2,\ldots,n_p\}$と定義し，影響感度を評価したい解析結果 $g=g(\boldsymbol{p})$を $\boldsymbol{p}$の期待値 $\bar{\boldsymbol{p}}$において 2次のTaylor近似で与えます． \begin{equation} \begin{split} &g(\boldsymbol{p})\approx g(\bar{\boldsymbol{p}})+\sum_{j=1}^{n_p}\dfrac{\partial g}{\partial p_j}(\bar{\boldsymbol{p}})(p_j-\bar{p}_j) +\dfrac{1}{2}\sum_{k=1}^{n_p}\sum_{l=1}^{n_p}\dfrac{\partial^2 g}{\partial p_k \partial p_l}(\bar{\boldsymbol{p}}) (p_k-\bar{p}_k)(p_l-\bar{p}_l) \end{split} \nonumber \end{equation} ここで，確率変数として定義された各材料パラメータ $p_i$($i=1,2,\ldots,n_p$)が互いに独立であるものとし，各々の確率変数が正規分布に従うものとすると，解析結果の期待値 $g$の期待値 ${\rm E}(g)$と分散 ${\rm Var}(g)$は，次式で近似評価できます． \begin{equation} {\rm E}(g)\approx g(\bar{\boldsymbol{p}}) +\dfrac{1}{2}\sum_{j=1}^{n_p}\dfrac{\partial^2 g}{\partial p_j^2}(\bar{\boldsymbol{p}})\sigma_{p_j}^2 \nonumber \end{equation} \begin{equation} \begin{split} &{\rm Var}(g)\approx \sum_{j=1}^{n_p}\biggl( \dfrac{\partial g}{\partial p_j}(\bar{\boldsymbol{p}})\biggr)^2\sigma_{p_j}^2 +\dfrac{1}{4}\biggl[ 3\sum_{j=1}^{n_p}\biggl( \dfrac{\partial^2 g}{\partial p_j^2}(\bar{\boldsymbol{p}})\sigma_{p_j}^2\biggr)^2 -\sum_{k=1}^{n_p}\sum_{l=1}^{n_p}\dfrac{\partial^2 g}{\partial p_k^2}(\bar{\boldsymbol{p}}) \dfrac{\partial^2 g}{\partial p_l^2}(\bar{\boldsymbol{p}})\sigma_{p_k}^2\sigma_{p_l}^2 \biggr] \end{split} \nonumber \end{equation} なお，$\sigma_{p_j}$は $p_j$の標準偏差であり，解析結果の標準偏差 $\sigma_g$は $\sigma_g=\sqrt{{\rm Var}(g)}$で評価できます．
　さて，上記の方法を用いて，材料パラメータの変動が繰り返し変形解析結果に及ぼす影響について評価してみます． ここでは，バラスト材の大型繰り返し三軸試験を想定し，拘束圧 $\sigma_c=-41.3$(kPa)，$n=(-q/p)_{cyc}/(-q/p)_{max}=0.93$として順解析を行ないました． まず，弾性挙動に関する4種類の材料パラメータ $K_{ref}$，$p_{ref}$，$n^e$，$\nu$のいずれかが変動係数 10%の変動を有する場合における，主ひずみ $\kappa$と体積ひずみ $\varepsilon_{vol}$の標準偏差を図 9に示します．$\kappa$や $\varepsilon_{vol}$に及ぼす影響が最も大きくなる $K_{ref}$の変動に対して，主ひずみ $\kappa$についてはその期待値の1%以下，体積ひずみについてはその期待値の 10%弱の変動量となることがわかります．

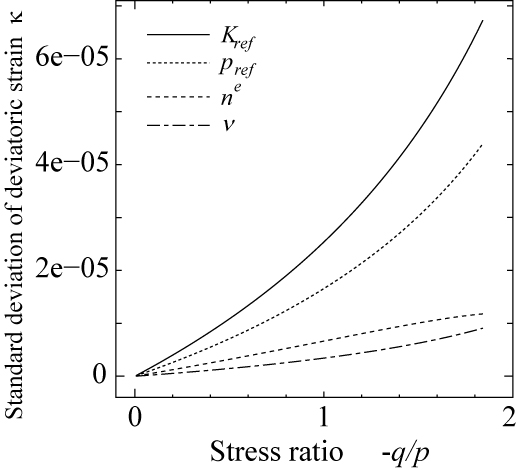
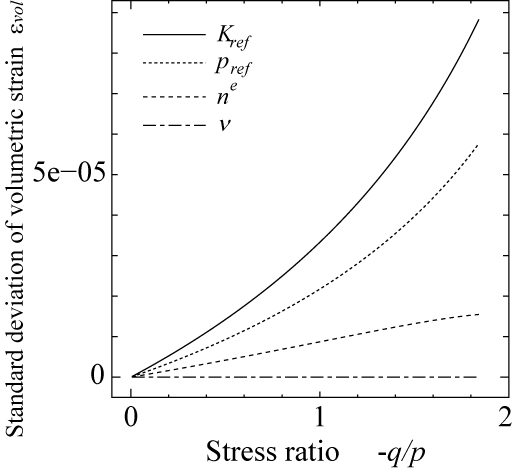(a) 主ひずみ $\kappa$の標準偏差（単調載荷過程）．　　　　　　 (b) 体積ひずみ $\varepsilon_{vol}$の標準偏差（単調載荷過程）．

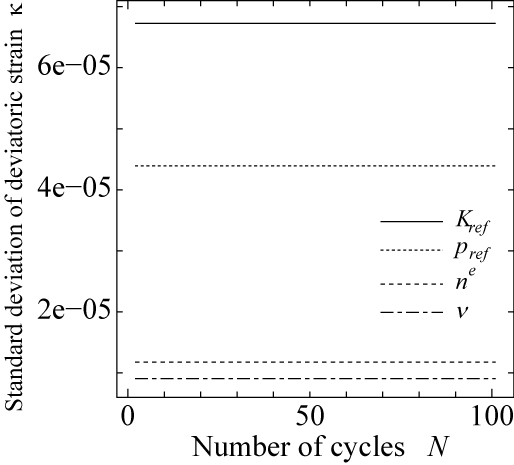
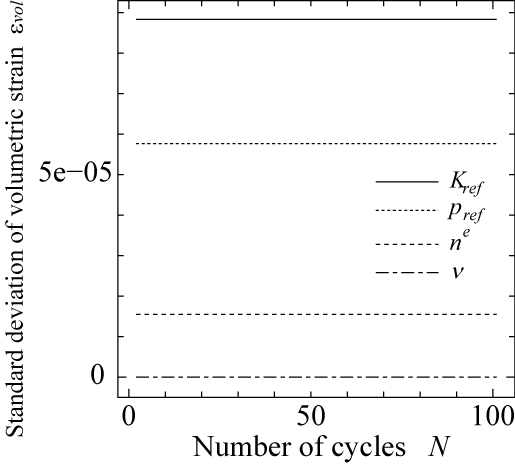(c) 主ひずみ $\kappa$の標準偏差（繰り返し載荷過程）．　　 (d) 体積ひずみ $\varepsilon_{vol}$の標準偏差（繰り返し載荷過程）．

図 9 弾性挙動に関する材料パラメータの変動が解析結果に及ぼす影響（拘束圧 $\sigma_c=-41.3$(kPa)）

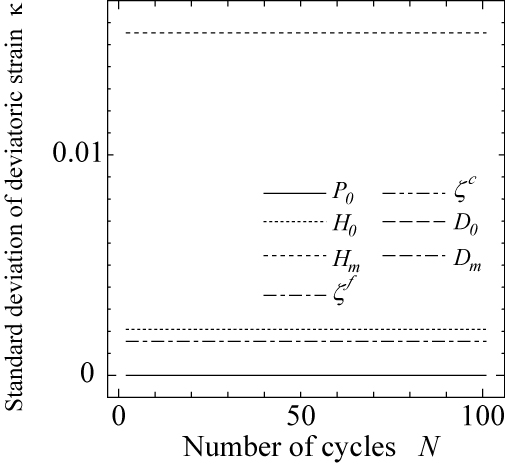
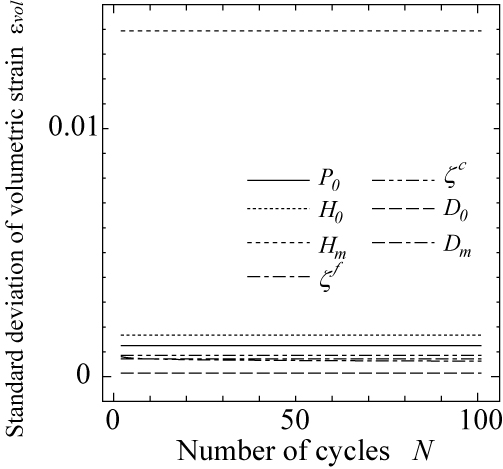
　単調載荷モデルの材料パラメータ $P_0$，$H_0$，$H_m$，$\zeta^f$，$\zeta^c$，$d_0$，$d_m$の7個のいずれかのみの変動（期待値の10%相当分）を考慮した場合における，主ひずみ $\kappa$と体積ひずみ $\varepsilon_{vol}$の標準偏差は，図 10に示す通りです．材料パラメータに10%の変動を考慮した場合，主ひずみや体積ひずみの解析結果は $H_m$の変動に対して最も鋭敏に反応し，最大主応力比 $(-q/p)_{max}=1.85$付近では，期待値の100%近いものとなっています．影響評価の対象となる材料パラメータのうち，$H_m$に次いで解析結果に及ぼすものは，摩擦すべりに起因した弾塑性挙動を表現するためのパラメータ $H_0$，$\zeta^f$であることがわかります．

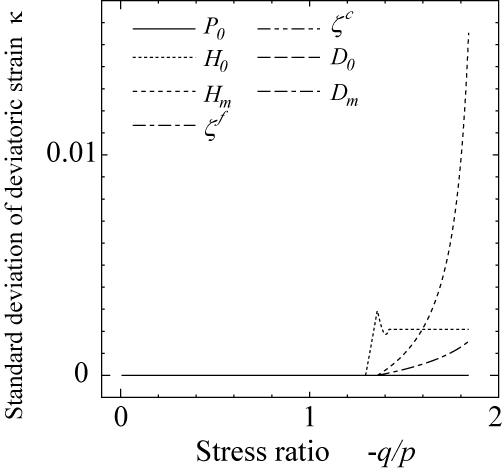
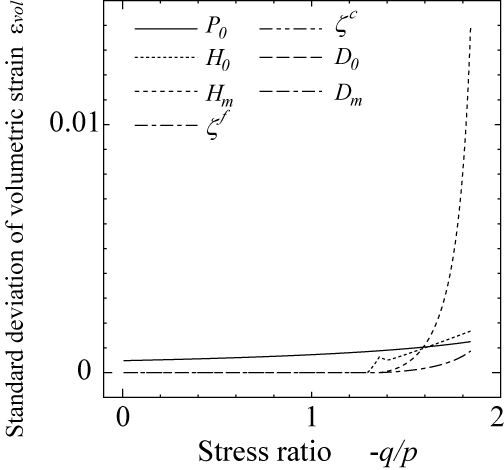(a) 主ひずみ $\kappa$の標準偏差（単調載荷過程）．　　　　　　 (b) 体積ひずみ $\varepsilon_{vol}$の標準偏差（単調載荷過程）．

(c) 主ひずみ $\kappa$の標準偏差（繰り返し載荷過程）．　　 (d) 体積ひずみ $\varepsilon_{vol}$の標準偏差（繰り返し載荷過程）．

図 10 単調載荷モデルの材料パラメータの変動が解析結果に及ぼす影響（拘束圧 $\sigma_c=-41.3$(kPa)）

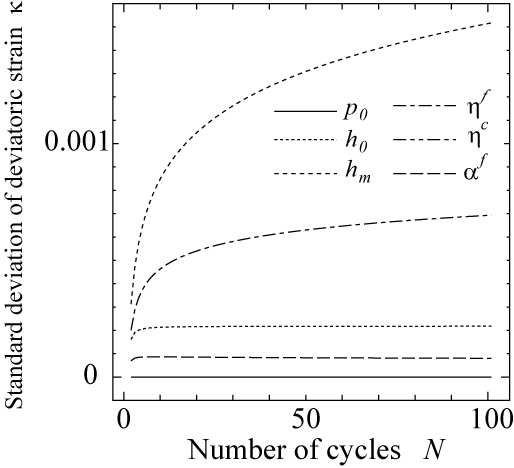
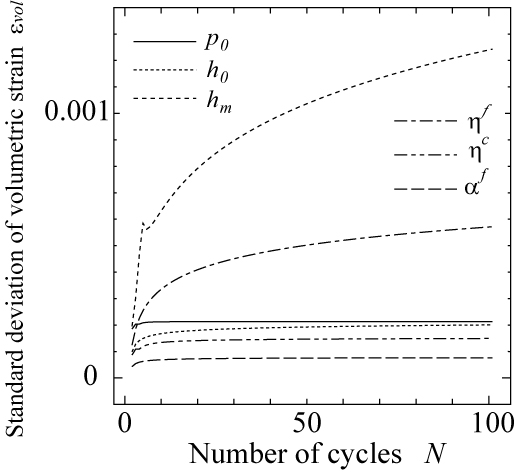
　最後に，繰り返し載荷モデルの材料パラメータである $p_0$，$h_0$，$h_m$，$\eta^f$，$\eta^c$，$\alpha^f$，$\alpha^c$，$\gamma^f$，$\gamma_c$，$d_0$，$d_m$ について，それらのいずれか一つにその期待値の10%相当の変動を考慮したときの主ひずみ $\kappa$，体積ひずみ$\varepsilon_{vol}$ の標準偏差を図 11に示します．変形解析結果への影響が比較的大きかったのは，$h_m$と $\eta^f$であり，これらのパラメータ値にその期待値の10%相当の変動が存在するとき，変形解析結果の変動は，最大でも数%〜10%程度で推移しています．この比率は，荷重作用の繰り返しに伴い塑性変形が蓄積し $\kappa$や $\varepsilon_{vol}$の値が増加しても，概ね一定な値を示すことがわかります． 以上の結果から，実験結果等から cyclic densificationモデルの材料パラメータを決定する上で最も注意が必要なのは，材料の内部摩擦角に相当する $H_m$，$h_m$であると考えられます．
 

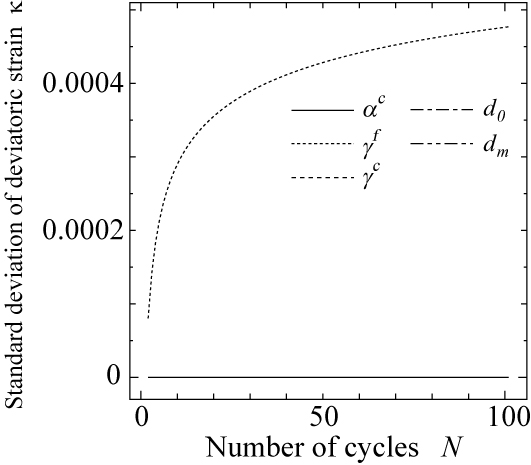
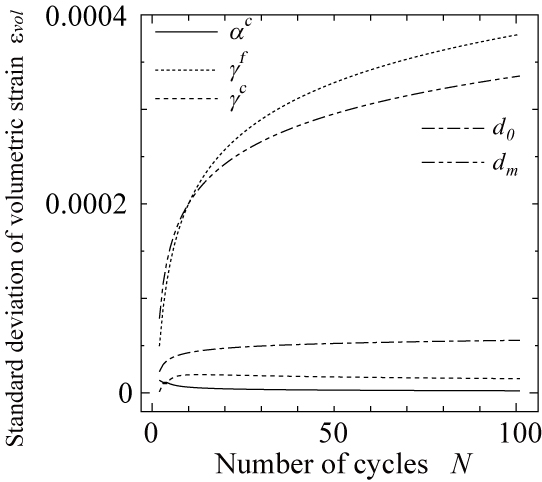(a) $\kappa$ の標準偏差．　　　　　　　　　　　　　　　　　 (b) $\varepsilon_{vol}$ の標準偏差．

図 11 繰り返し載荷モデルの材料パラメータの変動が解析結果に及ぼす影響 （拘束圧 $\sigma_c=-41.3$(kPa)）

　なお，本節で示した研究成果は，文献[6]として公表しています．
 

　上述のように，バラスト道床は層厚に対して粒径が小さくないこともあり，その力学応答には何らかの空間的なばらつきが存在し，その度合いは小さくないものと考えられます． バラスト道床沈下現象の弾塑性有限要素解析においては，実測結果とのカーブフィッティング等で連続体モデルの材料物性値を決定するため， 力学応答の空間的なばらつきの影響は材料物性値の空間変動として考慮するのが自然です． しかしこれまで，バラスト道床の力学モデルに用いる材料物性値の空間的なばらつきが軌道系各部の力学応答に及ぼす影響を評価した事例はほとんどなく， バラスト道床の Young率の空間的ばらつきが軌道系の振動応答に及ぼす影響を評価した Andersenら[7]や著者ら[8]の研究はありますが， 道床沈下解析結果に及ぼす影響は未検討となっていました．
　本研究では，cyclic densificationモデルを用いてバラスト道床沈下解析を行なう場合を対象に，バラスト材の Young率の空間的ばらつきが道床上面鉛直変位の解析結果に及ぼす影響を，スペクトル確率有限要素法(SSFEM)[9]を用いて評価します．スペクトル確率有限要素法の定式化では，Young率の空間的ばらつきを Karhunen-Loeve展開で表現した上で，確率空間における離散化の際に polynomial chaosを用います．なお，SSFEMを弾塑性問題へ適用するに際しては，定式化の煩雑さや計算負荷の増加を極力回避するために，Andersら[10]が提案した bounding body近似に基づく手法を用います．
　Young率の空間的ばらつきを表現するのに際し，まず，構成モデルにおいて線形弾性挙動を仮定して，弾性係数テンソルを次式で与えておきます． \begin{equation} \begin{split} D_{ijkl}&=E(\omega)\cdot D^*_{ijkl},\\ D^*_{ijkl}&=\dfrac{1}{2(1+\nu)(1-2\nu)} \bigl\{ (1-2\nu)(\delta_{ik}\delta_{jl}+\delta_{il}\delta_{jk})+2\nu\delta_{ij}\delta_{kl} \bigr\}, \end{split} \nonumber \end{equation} ここで，$E(\omega)$は空間的ばらつきを有する Young率であり，$\nu$は Poisson比，$\omega$は確率変数とします．そのため，弾塑性構成モデルにおける接線弾塑性係数 $D_{ijkl}^{(ep)}$は，$D_{ijkl}$と同様に次式で表わすことができます． \begin{equation} D^{ep}_{ijkl}=E(\omega)\cdot \Lambda_{ijkl}(D^*_{ijkl},\;\boldsymbol{\sigma}(\omega),\;\boldsymbol{q}(\omega)), \nonumber \end{equation} ここで，$\boldsymbol{q}$は内部状態変数であり，$\Lambda_{ijkl}$は $E$と乗じること接線弾塑性係数テンソルを構成する4階テンソルとします．上式では，その材料非線形性ゆえに確率論的変動を有する Young率 $E$，応力 $\boldsymbol{\sigma}$および内部状態変数 $\boldsymbol{q}$に依存して決まるため，確率空間での近似・離散化が困難であることから， bounding body近似[10]を導入すると，次式を得ます． \begin{equation} D^{ep}_{ijkl}=E(\omega)\cdot \Lambda_{ijkl}(D^*_{ijkl},\;\boldsymbol{\sigma}^{\pm},\;\boldsymbol{q}^{\pm}). \nonumber \end{equation} なお，$\boldsymbol{\sigma}^{\pm}$, $\boldsymbol{q}^{\pm}$は，物体の Young率がそれぞれ $\langle E^{-1}\rangle^{-1}$，$\langle E\rangle$（$\langle E \rangle$: $E$の期待値）で決定論的に与えられる弾塑性体である bounding body $V^+$および $V^-$において評価された応力および内部状態変数です．
　この弾塑性係数を仮想仕事式に代入し，有限要素法で離散化します．その際，Young率の空間的ばらつきを次式の Karhunen-Loeve展開で近似した上で \begin{equation} \begin{split} E(\boldsymbol{x},\omega)\approx \langle E \rangle \bigl[ 1+\alpha(\boldsymbol{x},\omega)\bigr],\hskip10mm \alpha(\boldsymbol{x},\omega)= \sum_{m=1}^{N_k} \xi_m(\omega) \sqrt{\lambda_m}\phi_m(\boldsymbol{x}), \end{split} \nonumber \end{equation} 第 $i$荷重ステップの第 $j$ Newton-Raphson反復における接線剛性行列を計算すると，次式のように評価できます． \begin{equation} \begin{split} &\bigl[\:^{j-1}\boldsymbol{K}_i(E(\omega),\;^{j-1}\boldsymbol{\sigma}_i(\omega),\;^{j-1}\boldsymbol{q}_i(\omega))\bigr] \approx \bigl[\:^{j-1}\boldsymbol{K}_i(E(\omega),\;^{j-1}\boldsymbol{\sigma}_i^{\pm},\;^{j-1}\boldsymbol{q}_i^{\pm})\bigr]\\ &\hskip20mm =\sum_{e=1}^{N_e}\int_{V_e}E(\omega)[\boldsymbol{B}^T][\boldsymbol{\Lambda}(\boldsymbol{D}^*,\;^{j-1}\boldsymbol{\sigma}_i^{\pm},\;^{j-1}\boldsymbol{q}_i^{\pm})][\boldsymbol{B}]dV\\ &\hskip20mm \approx \bigl[\;^{j-1}\boldsymbol{K}_i^{(0)}\bigr]+\sum_{m=1}^M \xi_m(\omega) \bigl[\;^{j-1}\boldsymbol{K}_i^{(m)}\bigr] \end{split} \nonumber \end{equation} \begin{equation} \begin{split} &\bigl[\;^{j-1}\boldsymbol{K}_i^{(0)}\bigr] =\sum_{e=1}^{N_e}\int_{V_e}\langle E \rangle[\boldsymbol{B}^T][\boldsymbol{\Lambda}(\boldsymbol{D}^*,\;^{j-1}\boldsymbol{\sigma}_i^{\pm},\;^{j-1}\boldsymbol{q}_i^{\pm})][\boldsymbol{B}]dV \end{split} \nonumber \end{equation} \begin{equation} \begin{split} &\bigl[\;^{j-1}\boldsymbol{K}_i^{(m)}\bigr] =\sum_{e=1}^{N_e}\int_{V_e}\langle E \rangle \sqrt{\lambda_m}\phi_m [\boldsymbol{B}^T][\boldsymbol{\Lambda}(\boldsymbol{D}^*,\;^{j-1}\boldsymbol{\sigma}_i^{\pm},\;^{j-1}\boldsymbol{q}_i^{\pm})][\boldsymbol{B}]dV \end{split} \nonumber \end{equation} さらに，接線剛性方程式の内力ベクトルは，その期待値で近似すると， \begin{equation} \Biggl[ \bigl[\;^{j-1}\boldsymbol{K}_i^{(0)}\bigr]+\sum_{m=1}^M \xi_m(\omega) \bigl[\;^{j-1}\boldsymbol{K}_i^{(m)}\bigr] \Biggr] \Bigl\{ \;^j\boldsymbol{\Delta U}_i(\omega) \Bigr\} =\bigl\{\boldsymbol{F}^{ext}_i\bigr\}-\Bigl\langle \;^{j-1}\boldsymbol{F}^{int}_i(\omega) \Bigr\rangle \nonumber \end{equation} となり，節点変位増分 $\{ \;^j\boldsymbol{\Delta U}_i \Bigr\}$を次式で定義される polynomial chaos展開により表現した上で， \begin{equation} \Bigl\{^{j}\boldsymbol{\Delta U}_i\Bigr\} \approx \sum_{l=0}^{L-1} \Bigl\{^j\boldsymbol{\Delta U}_i^{(l)}\Bigr\}\Psi_l(\boldsymbol{\xi}(\omega)) \nonumber \end{equation} polynomial chaos $\Psi_l$($l=0,1,\ldots$ $L-1$)を重みとした確率空間での Galerkin法を適用すると，各ステップで解くべき次の連立1次方程式を得ます． \begin{equation} \begin{split} &\sum_{l=0}^{L-1}\Bigl[ \delta_{ln} \bigl[\;^{j-1}\boldsymbol{K}_i^{(0)}\bigr] +\sum_{m=1}^M\langle \xi_m \Psi_l\Psi_n\rangle \bigl[\;^{j-1}\boldsymbol{K}_i^{(m)}\bigr] \Bigr] \Bigl\{^j\boldsymbol{\Delta U}_i^{(l)}\Bigr\}%%%\\ %%%&\hskip15mm =\langle\Psi_n\rangle \bigl\{\boldsymbol{F}^{ext}_i\bigr\} -\langle\Psi_n\rangle \Bigl\langle \;^{j-1}\boldsymbol{F}^{int}_i(\omega) \Bigr\rangle \end{split} \nonumber \end{equation} ただし，$n=0,1,\ldots,L-1$とします．
　解析では，バラスト道床として図 12に示す解析領域を考えます． 解析領域は，まくらぎ間隔 0.6mとして幅0.24mのまくらぎ5本を配置する領域を設定し，各まくらぎ位置ではまくらぎ幅で等分布に作用する表面力を与えました． 各まくらぎ位置での表面力の大きさは，領域中央でのまくらぎ位置に作用する表面力の合力は61.4kN，中央まくらぎから離れるにつれて 40.6kN，12.7kNとなるように与えます． また，領域左右端の部分境界では面外変位拘束，領域底部の部分境界では完全変位拘束の各境界条件を設定しました．

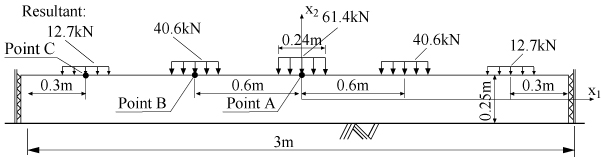図 12 バラスト道床を模擬した解析領域と荷重条件

Young率の空間変動成分の共分散関数 $C$は，$\sigma_E$を Young率の標準偏差，$b_1$，$b_2$をそれぞれ $x_1$軸，$x_2$軸方向の相関長さとして次式で与え， \begin{equation} C(\boldsymbol{x},\boldsymbol{\xi})=\sigma_E^2 \exp\Bigl[ -\dfrac{|\xi_1-x_1|}{b_1}-\dfrac{|\xi_2-x_2|}{b_2}\Bigr] \nonumber \end{equation} $E$の変動係数 $\delta_E=\sigma_E/\langle E\rangle=$1%または 15%にそれぞれ相当する値を与えて解析を行ない，$\sigma_E$の設定値が解析結果に及ぼす影響を考慮することとしました．一方，相関長さは $b=b_1=b_2=$0.2 または 2 (m)に設定しました．また，Karhunen-Loeve展開の項数は $M=4$，Polynomial chaosは1次の項まで考慮して展開項数を $L=5$としました．
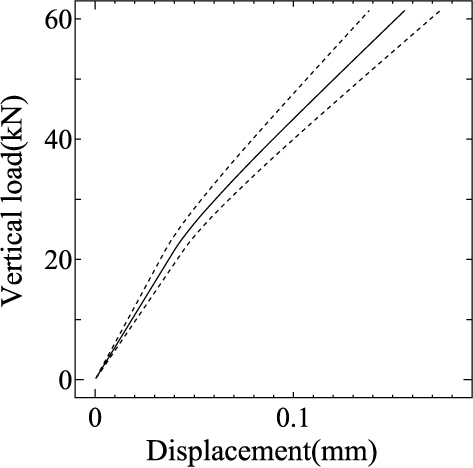
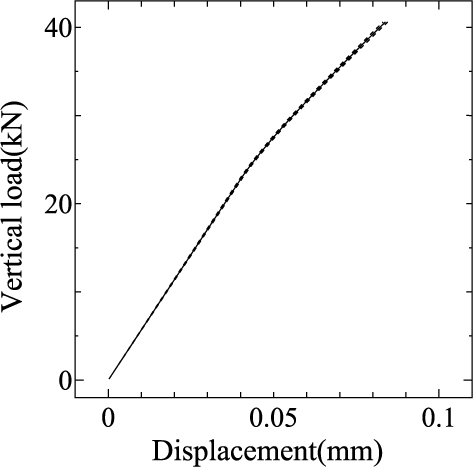
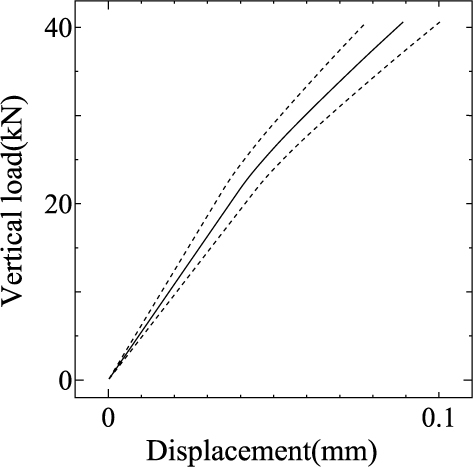
　まず，Young率の変動係数 $\delta_E$がバラスト道床上面変位およびその変動量（標準偏差）に及ぼす影響について検討してみます． 図 13は，$\delta_E=1$% または 15%に設定した場合の Point Aおよび Bでのバラスト道床上面鉛直変位の期待値と標準偏差を示したもので， 相関長さは $b=1$で一定としています．
 

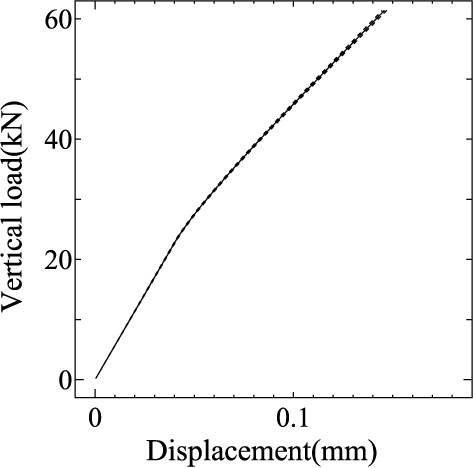
(a) $\delta_E=1$%　　　　　　　　　　　　　　　　　　　　　　　 (b) $\delta_E=15$%

(a) $\delta_E=1$%　　　　　　　　　　　　　　　　　　　　　　　 (b) $\delta_E=15$%

図 13 A点・B点における鉛直変位のばらつきに及ぼす Young率の変動係数の影響 （実線：期待値，点線：期待値 $\pm$ 標準偏差）

いずれの場合においても，Young率の空間変動の影響が伝播して生じるバラスト道床上面変位の変動量（標準偏差）は， Young率の変動係数とほぼ同等の割合で混入することがわかります．
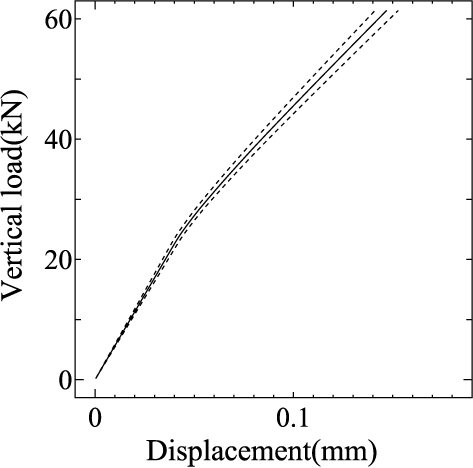
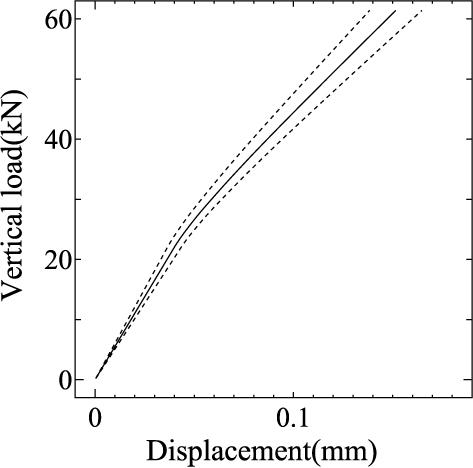
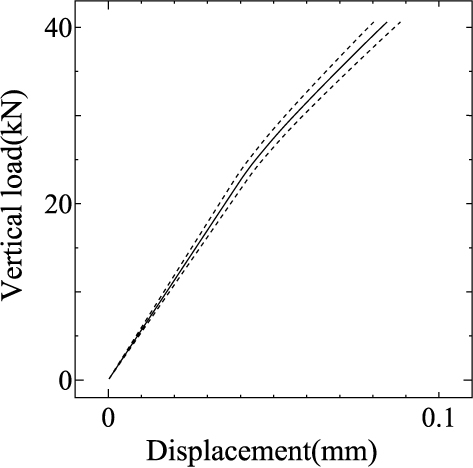
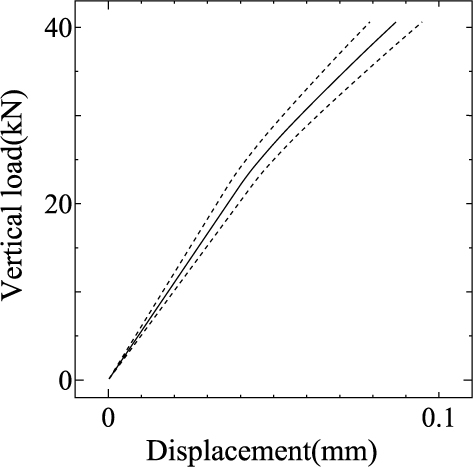
　また，Young率の空間変動に関する相関長さがバラスト道床上面変位の変動量（標準偏差）に及ぼす影響について検討してみます． 図 14は，相関長さを $b=0.2$(m) または 2(m)に設定した場合の Point Aでのバラスト道床上面鉛直変位の期待値と標準偏差を示したものです． なお，Young率の変動係数は $\delta_E=10$%で一定としています．
 

(a) $b=0.2$ (m)　　　　　　　　　　　　　　　　　　　　　 (b) $b=2$ (m)

(a) $b=0.2$ (m)　　　　　　　　　　　　　　　　　　　　　 (b) $b=2$ (m)

図 14 A点・B点における鉛直変位のばらつきに及ぼす Young率の変動に関する相関長さの影響 （実線：期待値，点線：期待値 $\pm$ 標準偏差）

相関長さをある程度大きな値に設定すると，道床上面変位の標準偏差は上面変位の期待値の10%程度となり，Young率の変動係数と同程度となっています． しかし，相関長さをバラスト道床厚程度である0.2(m)に設定すると， 入力情報に含まれる Young率の空間変動から道床上面鉛直変位の変動量に伝播する不確実性は相対的に小さくなることがわかります．
 
　なお，本節で示した研究成果は，文献[11]として公表しています．
 

　準備中です．

　準備中です．

　準備中です．