はじめに
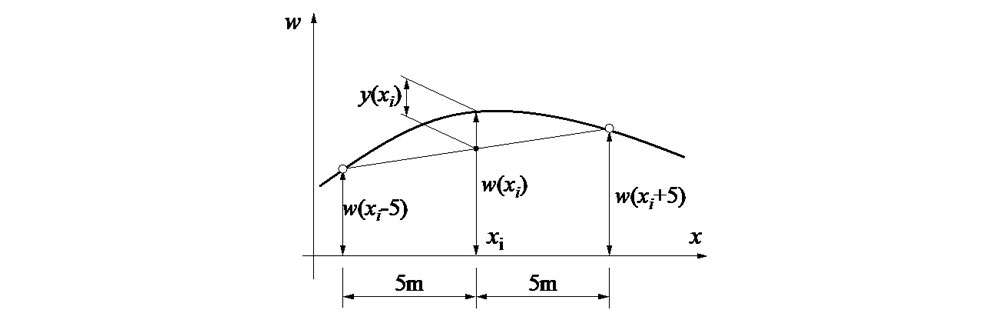
軌道の通り変位の管理は,それ自体の幾何形状(原波形)や振幅ではなく,一般に10m弦正矢と呼ばれる値に基づいてなされる.なお,10m弦正矢は,図-1 に示す様に,着目点xiにおける通り変位原波形値w(xi)と,そこから前後5m離れた2地点における通り変位原波形w(xi-5),w(xi+5)とを結ぶ直線上(弦)の中点xiにおける値との差yiで与えられる.軌道保守過程で10m弦正矢に基づき通り変位補正が行われた場合,それが許容値以下に修正されることで,間接的に原波形振幅やその標準偏差などが低減され,その結果,座屈確率も改善されるものと考えられるが,文献[2], [3]ではその実際の効果は未確認なままである.
そこで,初期通り変位原波形に10m弦正矢の許容値に基づいた補正を加え,それが軌道座屈確率に及ぼす影響について調べる.なお従来,10m弦正矢の補正法として交差法と呼ばれるものが用いられており,その改良法なども提案されている.当該法では,5m間隔に配置された各点での10m弦正矢の修正量が求められる.しかし本研究では,座屈解析を行う過程で,各有限要素節点における通り変位原波形自体の補正量を直接求める必要がある.そのため,各節点における10m弦正矢値が許容値以下となる様な通り変位原波形の補正量を求めるための一連の過程を最適化問題として定式化し,それに基づく新たな補正法を構成した.
10m弦正矢許容値に基づく通り変位原波形補正法
2.1 10m弦正矢と通り変位原波形との関係式
レールをはり要素で分割する際に,i番節点の軌道長手方向座標値をxi=iΔxで与えるものとする.なお,Δxはx方向の節点間隔である.n=5/Δxとおくと,i番節点から前後に5m離れた節点の番号はi±nで与えられる.すると図-1に示した10m弦正矢y(xi )=yiは次式で与えられる.
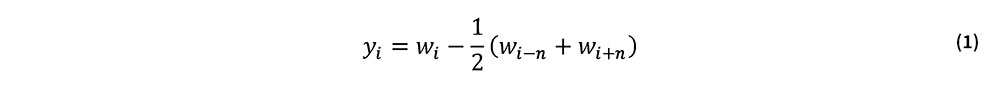
ここで,wiはi番節点における通り変位原波形値である.式(1)より,yiとwiを成分に持つベクトル{Y}と{W}との関係は,次式の様に表すことができる.
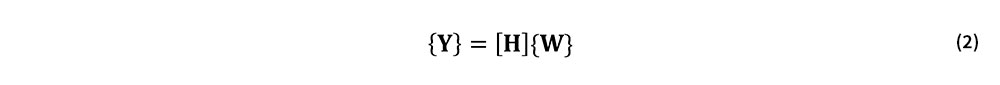
ここで,{W}がw1,⋯,wMを成分に持つものとすると,{Y}の成分はyn+1,⋯,yM-nで与えられることとなる.また,[H]は,式(1)に基づいて定まる長方形行列である.
2.2 初期通り変位原波形の補正計算
ここでは,補正前の初期通り変位原波形と,それに対する10m弦正矢の節点値を改めてw0i,y0iで与える.また,そこからの補正量をそれぞれwi,yiで与える.前述のとおり,通り変位は10m弦正矢に基づいて管理がなされる.その過程を再現するために,各節点における10m弦正矢の絶対値|y0i+yi |が,その許容値ymax以下となる様な,初期通り変位原波形節点値の補正wiを求めたい.本研究では,この操作を次の目的関数Jの最小化問題として定義する.
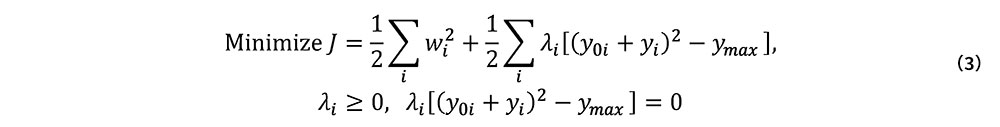
ここで,λiは未定乗数ベクトル成分である.
目的関数の主要部分は式¥eqref{eq10}の右辺第1項目であり,通り変位原波形の補正量を最小限に抑えるために設けたものである.
右辺第2項は,10m弦正矢の許容値に関する制約条件である.その具体的な値は本来恒等的にゼロとなるので,Jの値は右辺第1項目により与えられる.
Jのwiに関する感度は次式で与えられる.
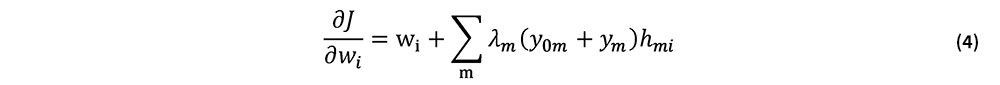
ここで,hmiは式(2)の行列[H]の成分である.
wiの最適解を勾配法により求める.その際の修正量Δwiは次式により与えるものとする.
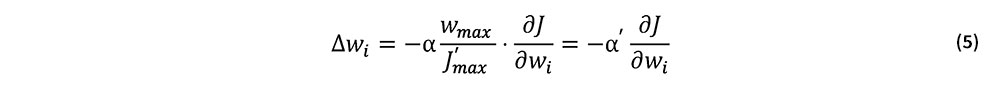
ここで,αは正の定数,wmaxとJ'maxはそれぞれwi,および∂J/∂wiの絶対最大値である.
次に,未定乗数ベクトル成分λiの導出について述べる.ある節点iにおいて|y0i+yi |>ymaxであるとき,次式を満たす様にyiの修正量Δyiを設定する.
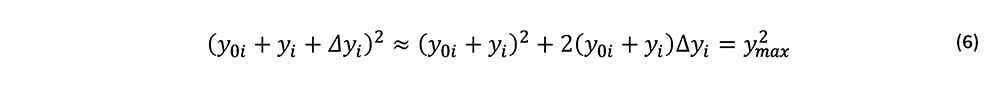
式(6)をΔyiについて解くと次式を得る.
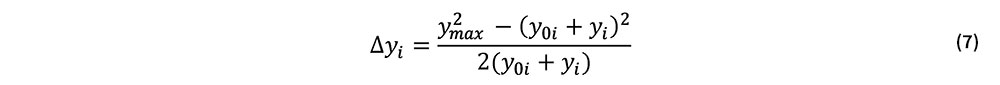
式(2)より,ΔyiとΔwiとの関係は次式で与えられる.
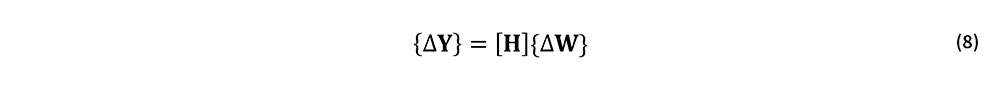
一方,式(4), (5)より,Δwiは次式で与えられている.
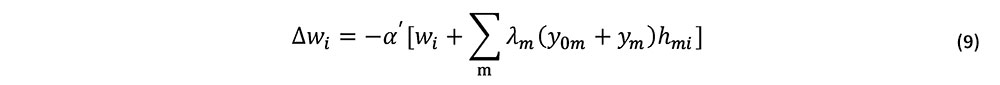
式(7), (9)を式(8)に代入すると,λiに関する次の連立方程式を得る.
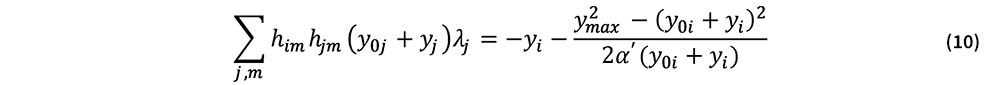
式(10)を解くことで未定乗数λiが求められる.
結果
3.1 解析条件
50kgNレールで構成されるロングレール軌道を想定する.まくらぎ間隔は0.6 mとし,軌道長720 m (まくらぎ1200本)をモデル化して,まくらぎ支持点間のレールをはり要素で2分割して離散化した.本解析における要素長はそれに比べ十分に短く,よって当該要素分割数が結果に影響を及ぼす恐れは無い.なお,この条件では5/Δxは約16.7となり,整数値を与えない.そこで以下の解析では,式(1)のnを17に設定した.この場合,弦長は10.2mとなるが,10mとの差は僅かであるため,当該条件での結果を10m弦正矢に基づく補正と見なすこととした.
ランダムな初期通り変位を作成する際の相関長は,過去の測定データに基づいた推定値d=2.84 mに設定した.また,以下の解析では,MCSのサンプル数を5000とした.なお,文献[2]のMCSでは,座屈確率が0.1%程度であればサンプル数を1000とした場合と5000とした場合との差異は比較的小さかった.
3.2 軌道通り変位原波形補正法の有効性の確認
標準偏差σ=4mmの下,初期通り変位原波形を生成した.10m弦正矢値に対する許容値ymaxを4mmに設定して,2.に述べた手法により通り変位原波形補正を実施した.補正前後における10m弦正矢波形の一例を図-2 に示す.補正前の10m弦正矢には,10mmを超える箇所も存在している.一方,補正後の10m弦正矢は,設定した許容値であるymax=4mm以下に概ね抑えられており,本補正法の有効性が確認できる.なお,本解析では式(5)のαを0.2と設定した.また,通り変位原波形補正量wiを求める反復過程の収束判定は,次式で与えた.
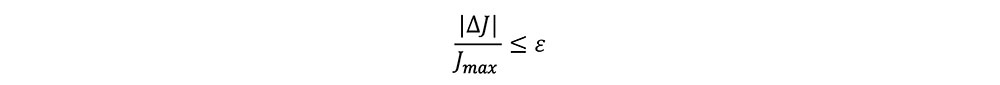
ここで,ΔJは目的関数Jの前修正ステップからの増分,Jmaxは現修正ステップまでにおけるJの最大値,εは収束判定値であり,本研究では0.01とした.なお,この条件下では,収束までに概ね20ステップを要した.
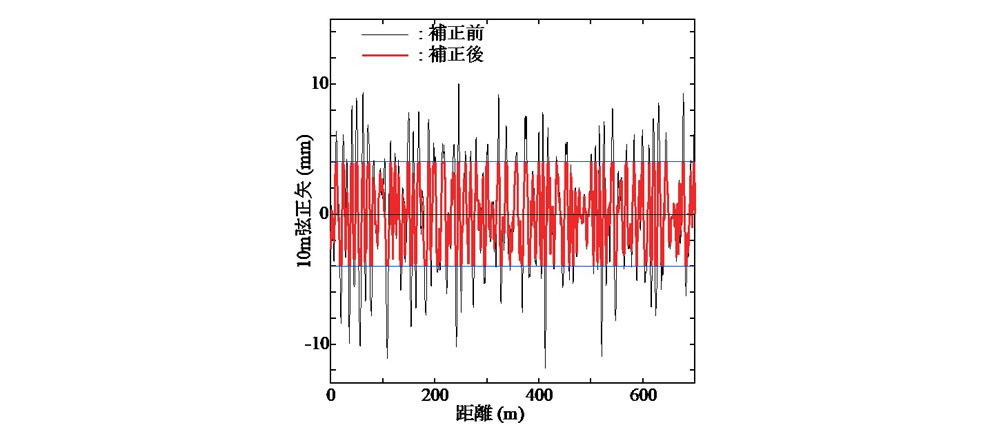
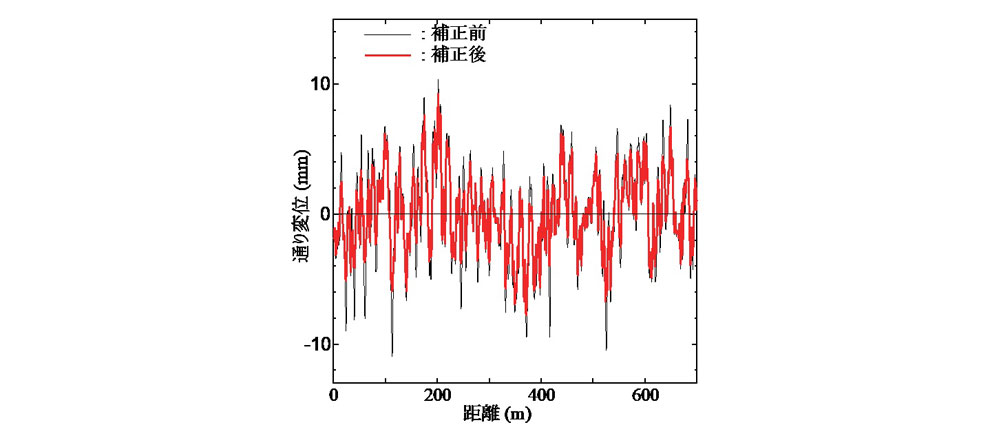
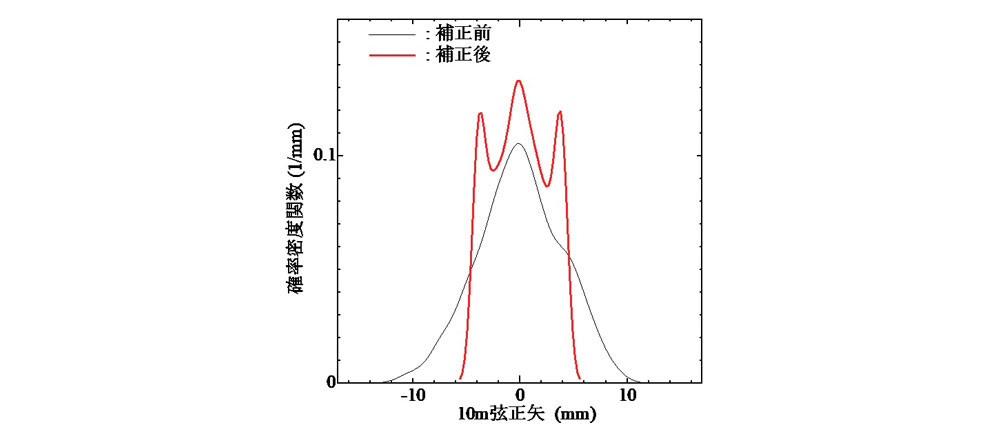
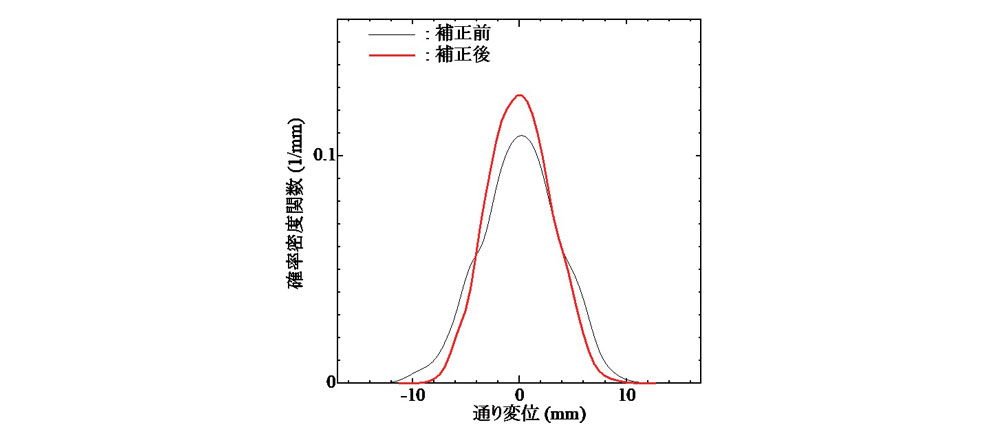
図-2の各10m弦正矢に対応する通り変位原波形を図-3に示す.10m弦正矢に基づく補正により,通り変位の振幅が全体に小さくなっている様子が確認できる.ただし,当然のことながら,通り変位原波形自体には,補正後も4mmを超える比較的大きな振幅が多くの箇所で認められる.
次に,10m弦正矢の許容値に基づく補正が,10m弦正矢波形や通り変位原波形の確率特性に及ぼす影響について調べる.まず,有限要素節点における10m弦正矢値の確率密度関数について,補正前後を比較した結果を図-4に示す.この図より,補正前は確率密度関数が広く分布していたものが,補正により概ね許容値以内に収められている様子が窺える.また,補正後は許容値近傍の確率密度関数が増大し,3箇所にピークが現れている.
続いて,補正前後における通り変位原波形の確率密度関数を図-5 に示す.図-3 では10m弦正矢許容値に基づく波形補正によって原波形の振幅が縮小される様子を確認したが,図-5の確率密度関数の分布からもそのことが再確認できる.ただし,10m弦正矢に認められた様な,補正後における確率密度関数形状の著しい変化は認められない.ちなみに,σ=4mmで作成した初期通り変位原波形に対する補正後の標準偏差は2.9mmであった.
3.3 通り変位原波形補正が軌道座屈確率に及ぼす影響
初期通り変位原波形の標準偏差σ=4mm,10m弦正矢の許容値ymax=4mmのケースを対象に,通り変位原波形補正前後における座屈強度(温度)の確率分布関数を求めた結果を図-6に示す.この図には飛び移り座屈強度(実線)と最低座屈強さ(破線)の確率分布関数を示した.なお,当該軌道モデルの場合,軌道両端から200mを除く中央部の約300mが不動区間となっており,概ねこの範囲内で座屈が発生する.実際の軌道では,一定距離(例えば1km)当りの座屈確率を基準に管理するのが適切であると考えられるが,異なる区間長での座屈確率は図-6の結果から容易に換算可能[2]である.
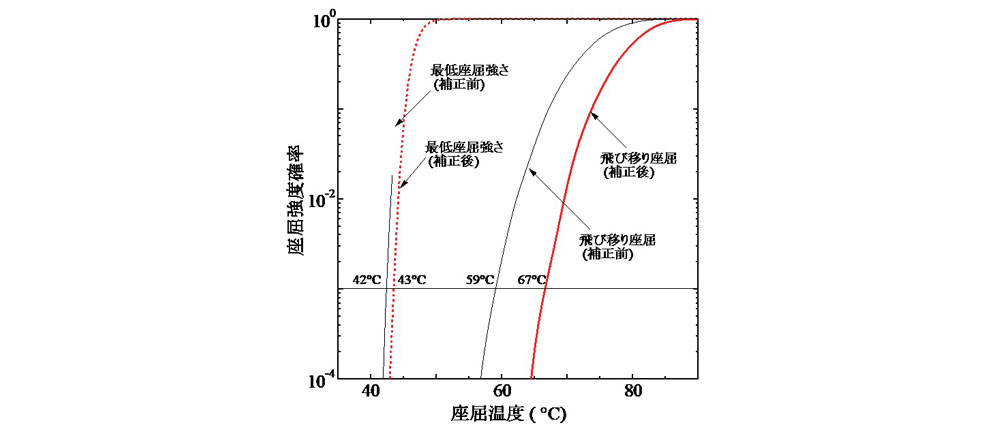
図-6より,通り変位原波形の補正により,飛び移り座屈強度が大幅に向上する様子が確認できる.例えば,座屈強度確率0.1%で比較すると,通り変位原波形補正により座屈温度は59℃から67℃にまで上昇しており,10m弦正矢の許容値に基づく波形補正が座屈強度向上に有効に作用することがわかる.一方,最低座屈強さの場合,飛び移り座屈強度とは異なり,通り変位原波形補正の前後において1℃程度しか変化していない.その結果,最低座屈強さと飛び移り座屈強度との差で与えられる座屈余裕度は,通り変位原波形補正によって17℃から24℃にまで増加しており,最低座屈強さに基づいた管理基準値のより大幅な緩和が期待できる.
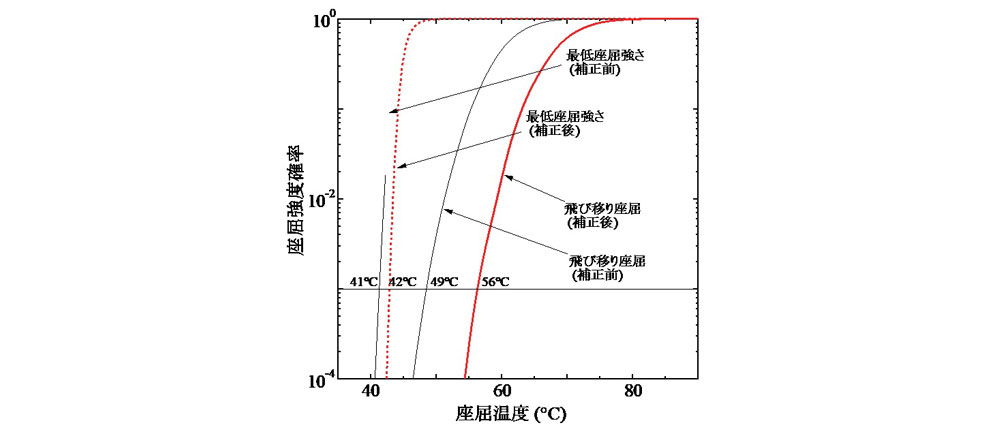
次に,初期通り変位原波形の標準偏差が6mmのケースにおける座屈強度の確率分布関数を図-7に示す.なお,10m弦正矢の許容値は4mmのままである.図-7より,10m弦正矢許容値に基づく通り変位原波形補正によって,σ=4mmの場合と同様に,飛び移り座屈強度が大きく向上することが確認できる.ただし,その向上度はσ=4mmのケースと同程度であるものの,初期通り変位の標準偏差が2mm増加したことで確率分布関数自体が低温側に移動しており,座屈余裕度は補正後であっても14℃と相対的に低めとなっている.このことから,座屈余裕度は補正前の通り変位波形振幅に大きく依存することがわかる.
おわりに
10m弦正矢が許容値以下となる様に通り変位原波形を補正することが,必ずしも原波形自体の振幅低減に直結するとは限らないため,その操作がどの程度軌道座屈強度の改善につながり得るのかが明らかではなかった.そこで補正前後における軌道座屈強度の確率分布関数をMCSより求めた.その結果,飛び移り座屈強度に関して大幅な向上が認められ,10m弦正矢に基づく補正が座屈強度改善に有効であることが確認できた.
参考文献
- 阿部和久,新井 優介,紅露一寛 : 軌道通り変位補正が座屈確率に及ぼす影響,計算数理工学論文集,
- 阿部和久,水野雄太,紅露一寛 : 通り変位波形におけるバラツキが軌道座屈強度の確率特性に及ぼす影響,鉄道工学シンポジウム論文集,No.24, 167-174, 2020.
- 岩井 翔,阿部和久,紅露一寛 : 通り変位と道床横抵抗力のバラツキを考慮した軌道座屈余裕度の確率的評価,鉄道工学シンポジウム論文集,第25号,69-76, 2021.