解析条件
座屈解析に当り,50kgNレールで構成される軌道を想定し,水平面内(弱軸回り)曲げ剛性を663 kN⋅m2,伸び剛性を1.32 GNと設定した.また,線膨張係数は12×10-6(1/℃) とした.まくらぎ間隔は0.6mとし,軌道長720m (まくらぎ1200本)をモデル化して,まくらぎ支持区間のレールをはり要素で2分割して離散化を行った.その際に,軌道両端は固定せず,温度伸縮や座屈過程での軌道変位を許容する様にした.
その他,レール・まくらぎ締結バネと道床抵抗力に関する諸量は,既往の研究等[3]を参考に表-1 に示すとおり設定した.なお,最終道床横抵抗力f0Tはまくらぎ1本分,最終道床縦抵抗力f0Lはレール1本分(まくらぎ1/2本分)の値である.以下の解析では,表-1を基本設定として用いるが,道床横抵抗力の変動が座屈確率に及ぼす影響を検討する際は,f0Tのみ異なる設定に変更する.
ランダムな初期通り変位を作成する際の相関長は,過去の測定データに基づいた推定値d=1.7 mを基準とし,標準偏差σと合わせて適宜値を変え,それらが確率分布等に及ぼす影響について調べた.なお,文献[1]のMCSにおいて,座屈確率が0.1%程度であればサンプル数を1000とした場合と5000とした場合との差異が比較的小さかったことから,以下のMCSでもサンプル数を1000とした.
| 締結部横バネ定数 | kT (MN/m) | 40 |
|---|---|---|
| 締結部回転バネ定数 | kR (kN⋅m/rad) | 20 |
| 最終道床横抵抗力 | f0T (kN) | 5.5 |
| f0T/2を与える変位 | aT (mm) | 1.0 |
| 最終道床縦抵抗力 | f0L (kN) | 2.5 |
| f0L/2を与える変位 | aL (mm) | 1.0 |
初期通り変位波形の標準偏差が座屈確率特性に及ぼす影響
Ⅱ. 式(2)における初期通り変位波形の相関長dを1.7 mに固定し,標準偏差σを3~8 mmまで1 mm間隔で設定してMCSを実施した.飛び移り座屈温度と最低座屈温度の確率密度関数をそれぞれ 図-1 と 図-2 に示す.
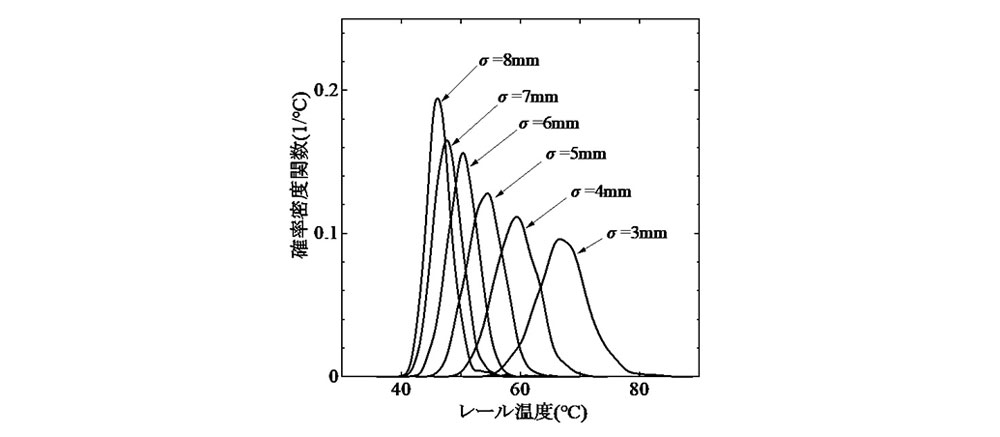
図-1 より,飛び移り座屈温度の最頻値は,初期通り変位波形の標準偏差の増加と共に低下しており,その度合いは標準偏差の値が小さい程顕著であり,座屈温度の初期不整鋭敏性が最頻値にも現れている.また,確率密度関数の広がり(分散)については,最頻値とは逆に標準偏差の増加と共に減少しており,確率密度関数の分布範囲が次第に狭まる傾向が確認できる.なお,飛び移り座屈温度の凡その下限値は約40℃と推定される.
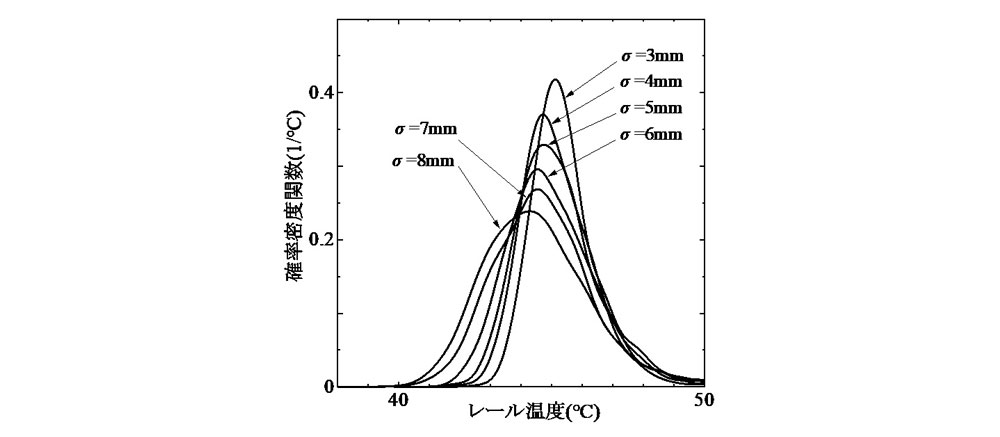
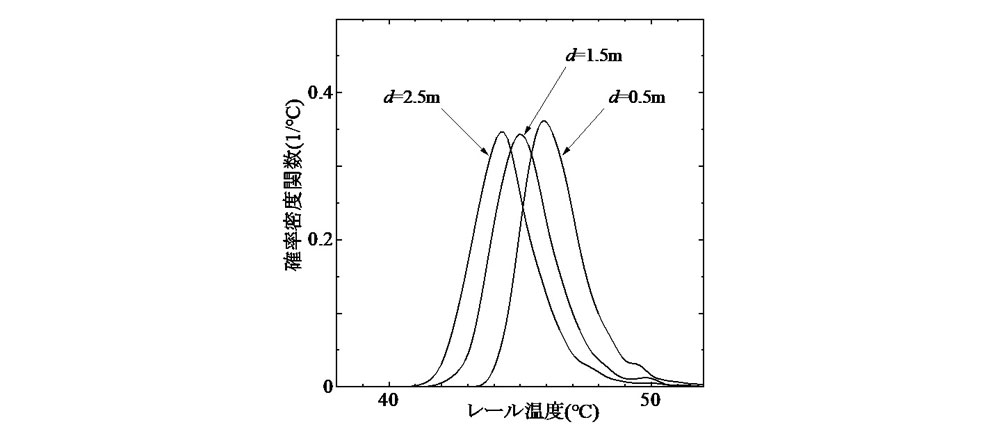
図-2 より,最低座屈温度の最頻値は,飛び移り座屈温度と同様に標準偏差の増加と共に低下することがわかる.ただし,飛び移り座屈温度の様な鋭敏性は認められない.また,標準偏差の増加に伴い分布範囲が拡大しているが,その変化は主に分布域下端で認められる.この図から,最低座屈温度の凡その下限値は約40℃と推定され,飛び移り座屈温度のそれとほぼ一致している.このことは,初期通り変位の標準偏差が比較的大きな軌道において,飛び移り座屈温度が極端に低いケースでは,それと最低座屈温度とがほぼ一致し,座屈余裕度が事実上存在しないことを示唆している.
(実線 : 飛び移り座屈,破線 : 最低座屈,d=1.7m)
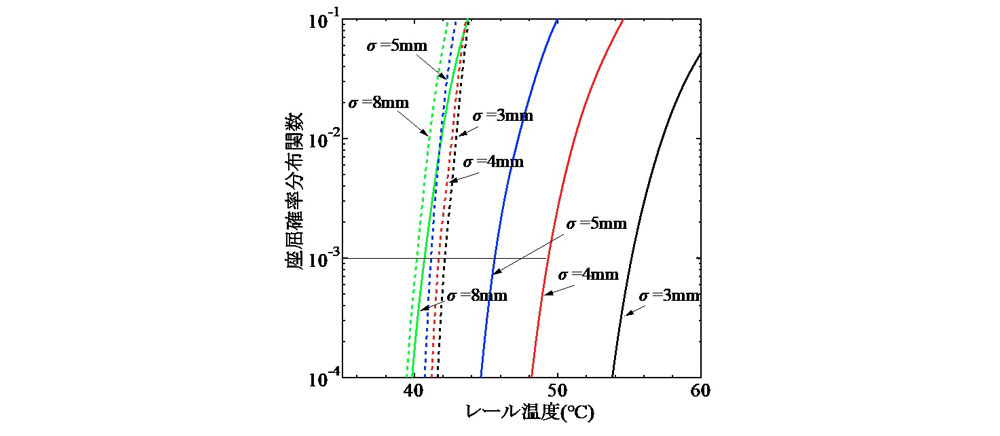
次に,飛び移り座屈温度と最低座屈温度の確率分布関数を 図-3 に示す.この図には,初期通り変位波形の標準偏差が3, 4, 5, および8 mmの4ケースを示した.飛び移り座屈温度の確率分布関数には,確率密度関数と同様に標準偏差の影響が顕著に現れている.例えば座屈確率P(t)=0.1%で比較すると,σ=3 mmと4 mmとではレール温度に6℃程度の違いが認められ,初期通り変位波形の標準偏差のわずか1 mmの違いが座屈確率に大きく影響することがわかる.
一方,最低座屈温度の確率分布関数に標準偏差が及ぼす影響は,飛び移り座屈温度に比べ非常に小さい.なお,図-2 より,確率密度関数について見ると,標準偏差の違いによる影響は低温側の裾近傍において比較的顕著に現れていた.しかし,図-3 に示した範囲の確率レベルであれば,σ=3 mmと8 mmとでの温度差は2℃程度であり,飛び移り座屈温度に比べ決して大きくはないことがわかる.
以上より,飛び移り座屈と最低座屈との温度差で与えられる座屈余裕度においては,標準偏差が飛び移り座屈温度に及ぼす影響が支配的となることが確認できた.ちなみに座屈発生確率0.1%で見ると,σ=3 mmでの座屈余裕度が12℃以上であるのに対し,σ=8 mmでは1℃以下となっている.
初期通り変位波形の相関長が座屈確率特性に及ぼす影響
初期通り変位波形の標準偏差をσ=5 mmに固定し,相関長dを変化させてMCSを実施した.dの値が飛び移り座屈温度と最低座屈温度の確率密度関数に及ぼす影響を,それぞれ 図-4 および 図-5 に示す.
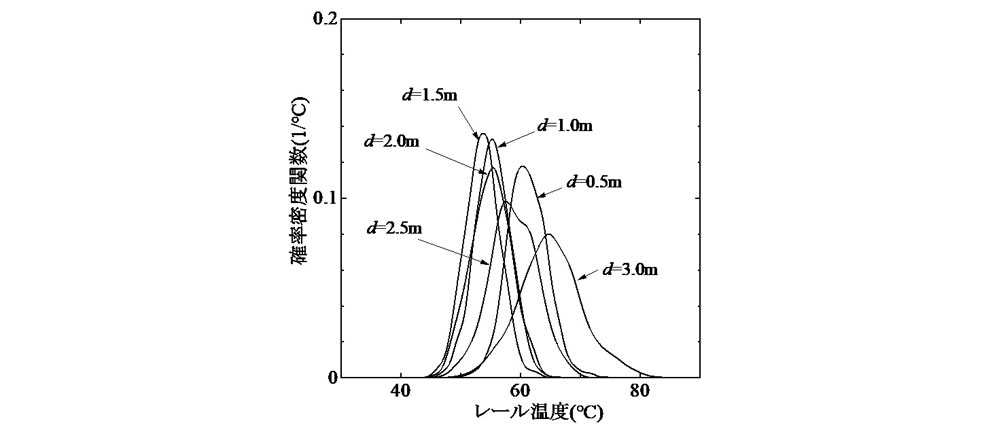
飛び移り座屈温度の確率密度関数の最頻値はd=1.5 m付近で最小となり,その前後では増加傾向を示す.これは,飛び移り座屈発生の際に成長し出すレールたわみの波数成分が,d=1.5 m前後のランダム波形に最も多く含まれていることによるものと考えられる.
一方, 図-5 の最低座屈温度の確率密度関数では,その最頻値はdの増加と共に一様に減少しており,飛び移り座屈温度とは異なる傾向を示している.なお,相関長についても,標準偏差と同様に,それが最低座屈温度の確率密度関数へ及ぼす影響は,飛び移り座屈温度のそれに比べて小さいことがわかる.
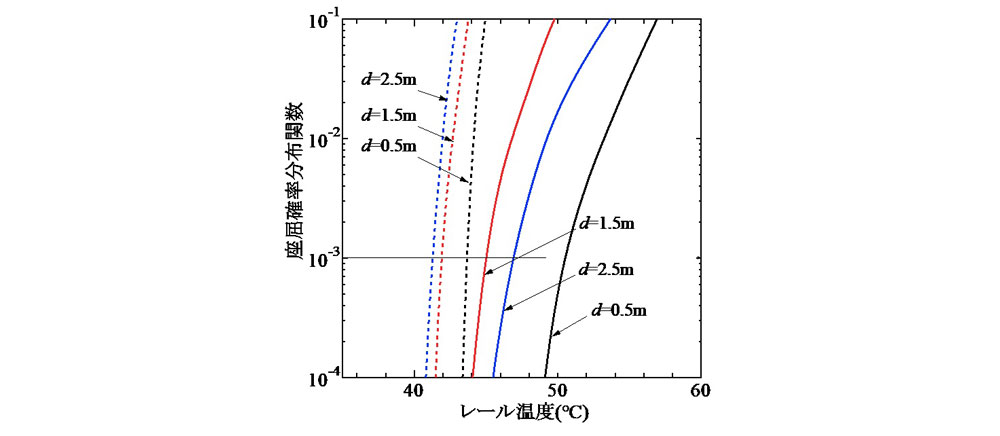
(実線 : 飛び移り座屈,破線 : 最低座屈,σ=5mm)
次に,飛び移り座屈温度と最低座屈温度の確率分布関数を 図-6に示す.この図には,初期通り変位波形の相関長dが0.5, 1.5, および2.5 mの3ケースを示した.確率密度関数と同様に,確率分布関数においてもdの違いによる影響は,飛び移り座屈温度の方が最低座屈温度に比べ幾分大きめに現れている.ただし,図-3に示した初期通り変位波形の標準偏差の影響と比べると,dによる飛び移り座屈温度の変化はやや小さく,最低座屈温度の変動幅と比べてそれ程顕著な違いは認められない.
d=1.5 m付近で飛び移り座屈温度の確率密度関数の最頻値が最小値をとることは既に述べたが,これと連動して確率分布関数においても同様の傾向が認められ,同一レベルの座屈確率で比較すると,対応するレール温度はd=1.5 mのケースが最も低くなっている.
一方,最低座屈温度の確率分布関数については,dの増加と共にレール温度は単調減少している.そのため,座屈余裕度はd=1.5 m付近で最小になるものと推測される.
初期通り変位波形の相関長が座屈余裕度に及ぼす影響
図-3 ,図-6 に示した結果より,飛び移り座屈温度と最低座屈温度との差で与えられる座屈余裕度を,座屈確率0.1%の場合を例に具体的に求めた.初期通り変位波形の相関長を1.7 mに固定して標準偏差と座屈余裕度との関係を求めたものを 図-7 に,標準偏差を5 mmに固定して相関長と座屈余裕度との関係を求めたものを 図-8に示す.
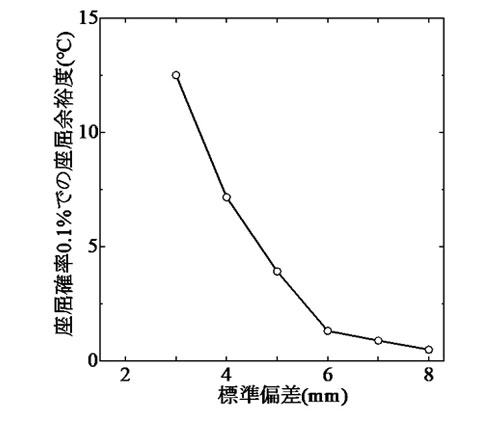
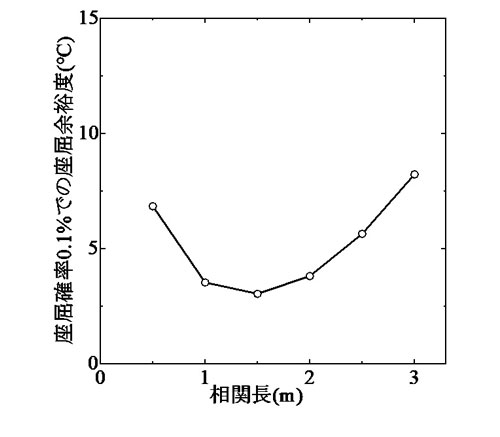
図-7より,初期通り変位波形の標準偏差による座屈余裕度への顕著な影響が確認できる.特に標準偏差の増加と共に座屈余裕度は急減少しており,飛び移り座屈温度の初期通り変位に対する鋭敏性が反映されている様子が窺える.具体的には,標準偏差が3 mmの場合の座屈余裕度が12.5℃であるのに対し,4 mmでは7.1℃,5 mmでは3.9℃,6 mmでは1.3℃となっている.現実の軌道における初期通り変位波形の標準偏差はこの範囲にあるものと考えられ,飛び移り座屈温度に基づく管理法を検討する際には,図-7の様な標準偏差に対する鋭敏性に十分留意する必要がある.
図-8に示した初期通り変位波形の相関長dと座屈余裕度との関係は,3. に述べたとおりd=1.5 m付近で最小値をとっている.なお,実軌道における通り変位波形の距離相関関数をⅡ. 式(2)で近似した場合の相関長は1.7 mと推定された.この値は 図-8で極小値を与えるd=1.5 mに近いことから,d=1.7 mの下で求めた 図-7は,各標準偏差における座屈余裕度の最低値を概ね示しているものと考えられる.従って,実際の初期通り変位波形の相関長がいかなる値を取ったとしても,各標準偏差の下で最低限確保し得る座屈余裕度は 図-7より把握可能である.
最終道床横抵抗力の空間変動が座屈確率特性に及ぼす影響
ロングレール軌道の座屈安定性評価における,道床横抵抗力のバラツキに対する考え方は[4]に示されている.しかし,その軌道長手方向への空間変動特性については不明な点が多い.そこで,最終道床横抵抗力に次式で示す空間変動を与え,その下で初期通り変位波形をランダムに設定してMCSを実施した.
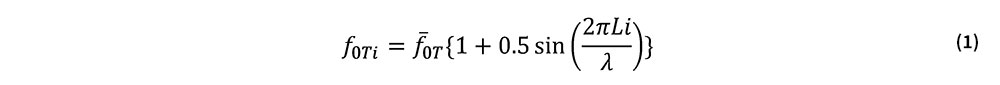
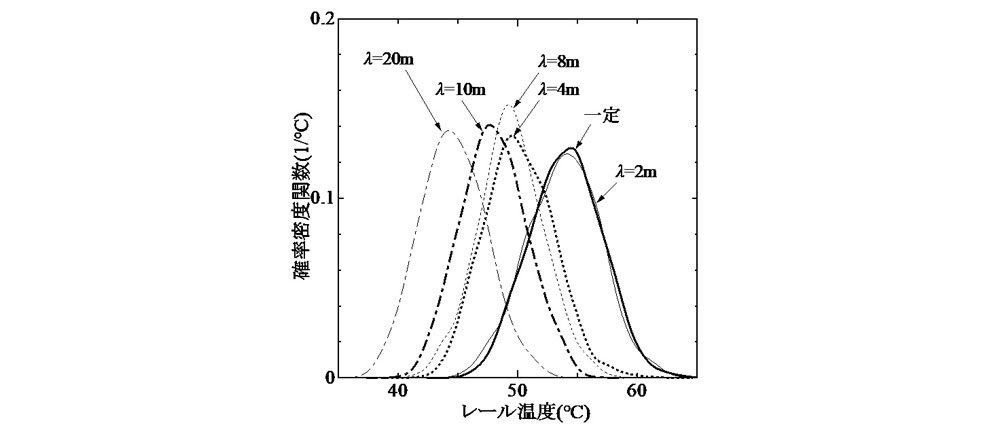
ここで,f0Tiは軌道モデル左端からi番目のまくらぎにおける最終道床横抵抗力,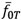 はそれらの平均値,λは空間変動波長である.なお,
はそれらの平均値,λは空間変動波長である.なお,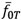 =5.5 kN/本とした.また,実軌道における変動振幅はせいぜい0.3
=5.5 kN/本とした.また,実軌道における変動振幅はせいぜい0.3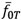 程度[4]と推定されるが,ここでは空間変動の影響を確認する目的で0.5
程度[4]と推定されるが,ここでは空間変動の影響を確認する目的で0.5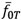 と大き目に設定した.
と大き目に設定した.
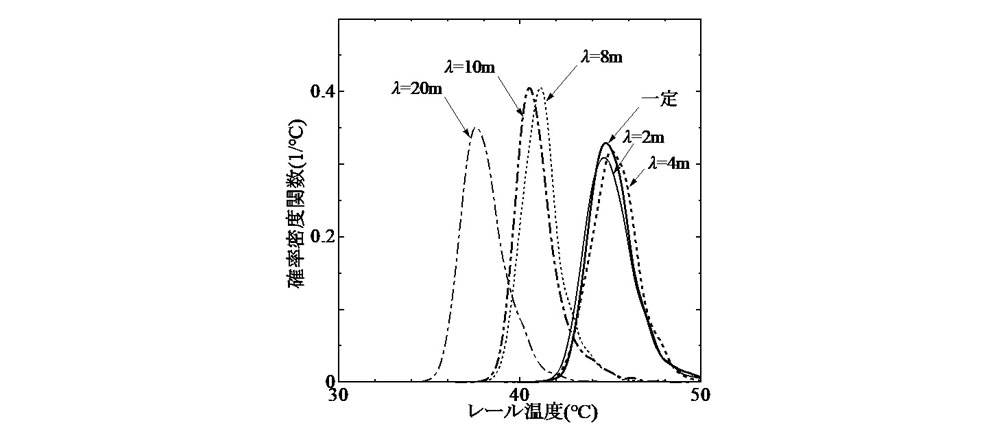
初期通り変位波形の標準偏差と相関長をそれぞれ5 mm,1.7 mとし,式(2)の変動波長を2~20 mまでの範囲で設定して得られた飛び移り座屈温度の確率密度関数を 図-9に示す.なお,図中には道床横抵抗力が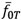 で一定値の場合も合わせて示した.λの増加と共に確率密度関数の分布域が低温度側へ移動する様子が確認できる.ただし,λ=2 mの結果は最終道床横抵抗力一定のものとほぼ一致しており,変動の影響は認められず,λ=4 mにおいて急激に変化している.また,λ=4~10 mの範囲における変化は,λ=2 mと4 mの両ケース間の変化に比べやや小さく,それ以上の波長域においても緩慢である.
で一定値の場合も合わせて示した.λの増加と共に確率密度関数の分布域が低温度側へ移動する様子が確認できる.ただし,λ=2 mの結果は最終道床横抵抗力一定のものとほぼ一致しており,変動の影響は認められず,λ=4 mにおいて急激に変化している.また,λ=4~10 mの範囲における変化は,λ=2 mと4 mの両ケース間の変化に比べやや小さく,それ以上の波長域においても緩慢である.
本軌道モデルにおける分岐座屈時の理論座屈波長は3.9 mであり,λ=4mに近い.軌道座屈過程では,この理論波長を起点として,たわみの増大と共により長波長の変位波形成分が成長する傾向が認められる[5].よって,λ=4m以下の波長成分は飛び移り座屈には影響を与えなかったものと解釈できる.一方,座屈たわみが集中して発生する箇所の区間長に比べより長い変動波長成分は,座屈区間全域の最終道床横抵抗力をほぼ一様に低下させる効果を持つため,それ以上変動波長を長くしても確率密度関数への影響は小さく,分布域は一定領域に漸近していくものと推測される.
次に,最低座屈温度の確率密度関数を 図-10に示す. 図-9の飛び移り座屈温度の確率密度関数と同様に,波長λの増加と共に分布域が低温側へ移動する様子が確認できる.ただし分布域の急変は,λ=4 mと8 mとの間で認められる.これは,飛び移り座屈時からさらに変位が進行した最低座屈点でのたわみ波形が,前述のとおり,より長い波長成分で構成されているためと考えられる.また,道床横抵抗力が一定値をとるケースとλ=20 mのケースとの間の最頻値低下量は,飛び移り座屈温度では約10℃であるのに対し,最低座屈温度では6℃程度となっており,前者の方が道床横抵抗力の空間変動波長に対する感度が高めとなっている.
最終道床横抵抗力のバラツキが座屈確率特性に及ぼす影響
5. の結果より,最終道床横抵抗力の空間変動により座屈温度が低下し,長波長成分程その効果が顕著に現れることがわかった.しかし,実軌道における空間変動の実態が明らかでない現状では,これ以上その影響について具体的に議論することは不可能である.そこで次に,最終道床横抵抗力が軌道長手方向に一定値を取りつつ,それが軌道毎にランダムな値をとる場合を想定し,初期通り変位波形に加え最終道床横抵抗力のバラツキも考慮して,それが座屈余裕度に及ぼす影響について調べることとする.
初期通り変位の標準偏差σ=5 mm,相関長d=1.7 mの下,軌道長手方向に一様な最終道床横抵抗力の値をサンプル毎にランダムに設定し,MCSを実施した.その際に,最終道床横抵抗力の確率密度関数pfを,次の4次のベータ分布により与えた.
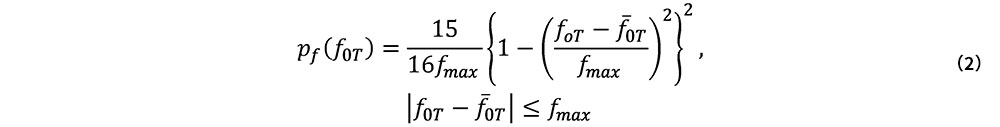
ここで,fmaxは最終道床横抵抗力の変動幅である.
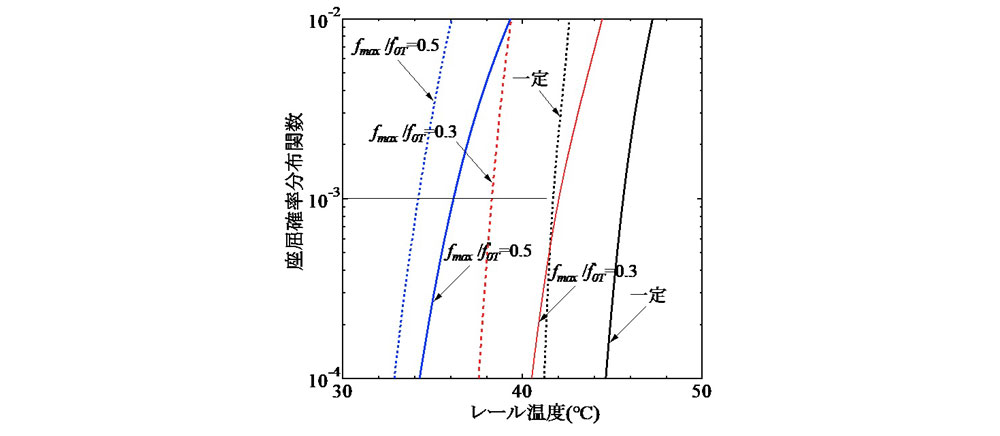
(実線 : 飛び移り座屈,破線 : 最低座屈,σ=5mm, d=1.7 m)
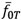 =5.5 kN/本の下,
=5.5 kN/本の下,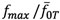 =0.0, 0.3, および0.5の3ケースに対して求めた飛び移り座屈温度と最低座屈温度の確率分布関数を 図-11に示す.最終道床横抵抗力の変動幅の増大に伴い,同一の座屈確率に対応する温度が低下する傾向が確認できる.
=0.0, 0.3, および0.5の3ケースに対して求めた飛び移り座屈温度と最低座屈温度の確率分布関数を 図-11に示す.最終道床横抵抗力の変動幅の増大に伴い,同一の座屈確率に対応する温度が低下する傾向が確認できる.
座屈確率0.1%における,最終道床横抵抗力の変動幅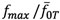 と,座屈余裕度との関係を 図-12に示す.この図より,変動幅
と,座屈余裕度との関係を 図-12に示す.この図より,変動幅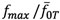 =0.4以下の範囲では,座屈余裕度は3~4℃程度の値で推移している.なお,座屈確率0.1%におけるMCSによる確率分布の計算精度は1℃程度[1]と推定され,
=0.4以下の範囲では,座屈余裕度は3~4℃程度の値で推移している.なお,座屈確率0.1%におけるMCSによる確率分布の計算精度は1℃程度[1]と推定され,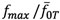 =0.4以下に見られる座屈余裕度の増減は,概ね誤差範囲内であると考えられる.よって,座屈余裕度における有意な低下は,少なくとも
=0.4以下に見られる座屈余裕度の増減は,概ね誤差範囲内であると考えられる.よって,座屈余裕度における有意な低下は,少なくとも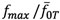 =0.4以上で生じ,最終道床横抵抗力の変動幅が極端に大きなケース以外では,それが座屈余裕度に及ぼす影響は比較的小さいものと思われる.
=0.4以上で生じ,最終道床横抵抗力の変動幅が極端に大きなケース以外では,それが座屈余裕度に及ぼす影響は比較的小さいものと思われる.
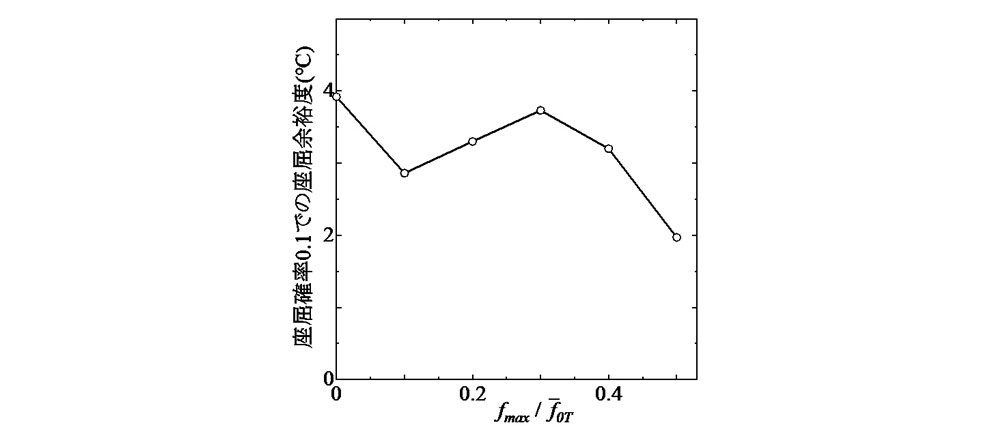
以上より,最終道床横抵抗力の変動は,所定の座屈確率に対応する温度低下をもたらすものの,座屈余裕度の低下への影響は限定的であることがわかった.
参考文献
- 阿部和久,水野雄太,紅露一寛 : 通り変位波形におけるバラツキが軌道座屈強度の確率特性に及ぼす影響,鉄道工学シンポジウム論文集,No.24, 167-174, 2020.
- 岩井 翔,阿部和久,紅露一寛 : 通り変位と道床横抵抗力のバラツキを考慮した軌道座屈余裕度の確率的評価,鉄道工学シンポジウム論文集,第25号,69-76, 2021.
- 西宮裕騎,片岡宏夫 : 座屈発生点を考慮したロングレールの座屈安定性の評価法に関する一考察,鉄道工学シンポジウム論文集,第20号,pp.9-15, 2016.
- 鉄道総合技術研究所 編 : 鉄道構造物等設計標準・同解説 軌道構造,11章 ロングレール,丸善出版,2012.
- 阿部和久,田中洋介,西宮裕騎,紅露一寛 : レール温度座屈時の分岐過程に関する一考察,鉄道力学論文集,No.13, pp.7-14, 2009.