はじめに
ロングレール軌道の座屈は鉄道における重大な事象の一つであり,従来から数理モデルに基づく検討がなされてきた[2, 3].しかし,座屈強度(温度)の定量的評価に主眼が置かれ,その発生機構や座屈強度と初期通り変位との関係などについては,解析結果に基づいた議論にとどまり,その理論的背景は必ずしも十分に理解されてこなかった様に思われる.また現在では,個々の軌道に対して,初期通り変位波形などの把握し得る様々な状態を精緻に再現した座屈解析も可能となっている.その様な状況下では,リアルな軌道状態を詳細に表現することができない簡易な理論モデルに基づいた評価は,もはや不要とも考えられる.しかし,上述の様な軌道座屈の理論的特性について理解しておくことは,数値解析結果の適切な評価や,軌道の合理的な座屈管理法を講ずる上で有用な知見となり得る.そこで以下では,軌道座屈に初期通り変位が及ぼす影響について理論的考察を行う.
軌道の数理モデル
直線ロングレール軌道を対象とする.道床横抵抗力を軌道に沿って連続分布する作用力として近似すると,左右レールから構成される軌道系の横方向変位(たわみ)に関するつり合い式は次式で与えられる.
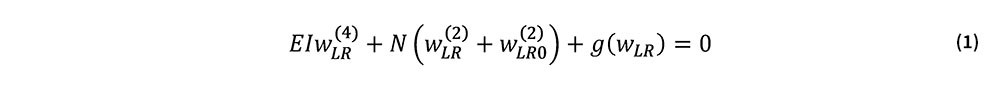
ここで,wLRは左右レールの弾性たわみの和,wLR0は左右レールの初期通り変位の和,( )(n)は軌道長手方向の座標xに関するn回微分を表し,EIはレール1本当たりの曲げ剛性,Nはレール軸力(圧縮を正),gはまくらぎを連続支持モデルで近似した際の単位長さ当たりに作用する道床横抵抗力(レール2本分)である.
道床横抵抗力gは,次の非線形性を有するものとする[3].
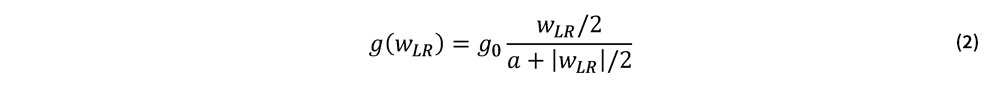
ここで,g0は最終道床横抵抗力,aはg=g0/2を与える変位(wLR/2)である.
座屈点近傍のつり合い解
座屈発生点前後のたわみが比較的小さな状態を対象とし,式(2)をwLR=0の近傍で次式により近似する.
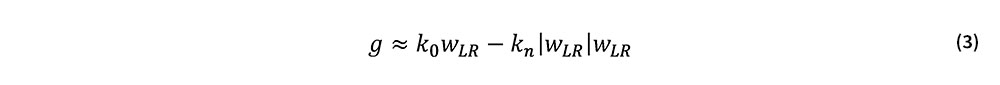
ここで,k0,knはそれぞれ式(2)のwLRに関する展開係数であり,具体的には次式で与えられる.
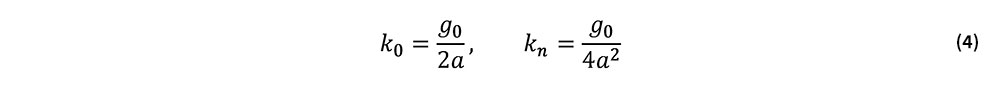
式(3)を(1)に代入すると次式を得る.
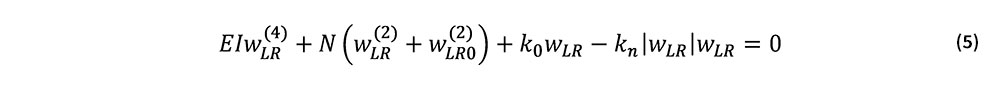
式(5)の初期通り変位として,次式で与えられる波数kの波形成分を考える.
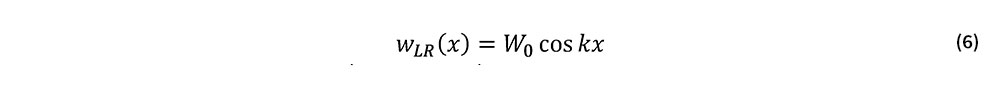
ここで,W0は波形振幅である.
式(5)では係数knに関する項がwLRの非線形項となっているので,式(6)の初期通り変位に対する解は本来k以外の波数成分も持つ.しかし以下では十分に小さな変位を対象とし,wLRの主要項が次式の様に波数kの成分で与えられるものと仮定する.
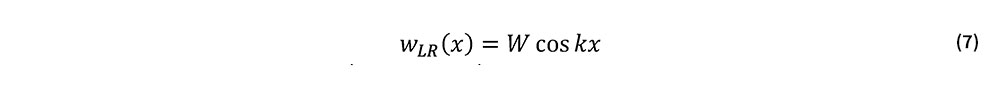
ここで,Wは変位振幅である.
式(6), (7)を(5)に代入して,|coskx | coskx≈8/3π⋅coskxと近似すると,つり合い解Wは次式の解として与えられる.
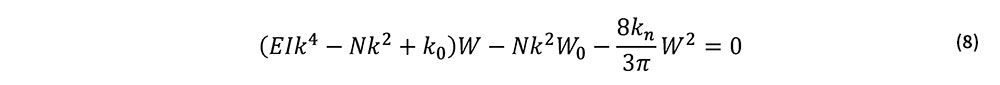
完全系のつり合い解
式(8)より,完全系(W0=0)のつり合い式は次の2式で与えられる.
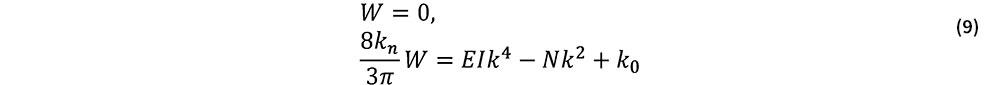
式(9)第2式より,自明な解W=0の基本つり合い経路上における分岐座屈軸力Ncrは次式で与えられる.
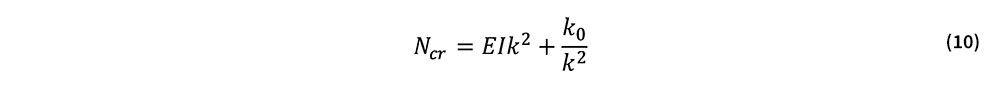
式(10)の座屈軸力は波数kに依存している.実際には,Ncrの最小値Nmが分岐座屈軸力を与える.式(10)より,Nmおよびその時の波数kmは次式で与えられる.
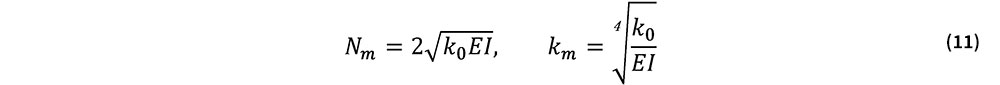
式(11)より,分岐座屈軸力と座屈モードの波数は,レールの曲げ剛性EIとwLR=0における道床横抵抗力の接線剛性k0で決まることがわかる.
また軸力Nを,式(10)の分岐座屈軸力Ncrとそこからの増分νに分離して,N=Ncr+νと表すと,式(9)第2式より次式を得る.
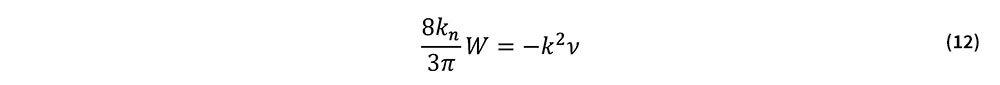
式(12)より,完全系における分岐座屈後のつり合い経路は次式で与えられる.
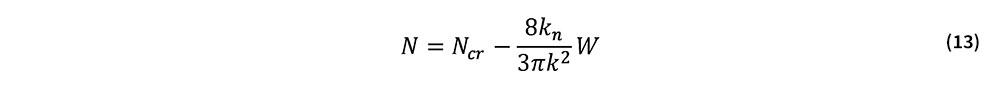
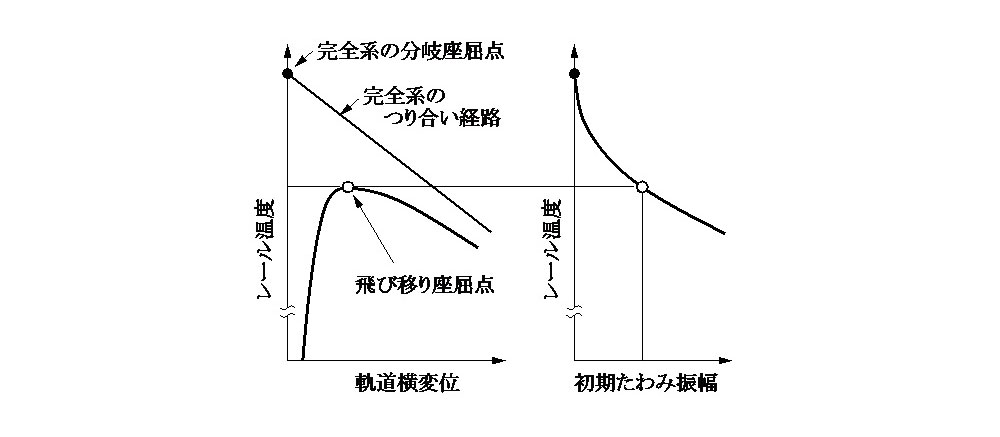
この分岐点からのつり合い経路は,図-1 に示した「完全系のつり合い経路」に対応するものである.
飛び移り座屈軸力の初期通り変位鋭敏性
初期通り変位振幅W0がゼロでない場合について考える.式(8)において,N=Ncr+νとおくと次式を得る.
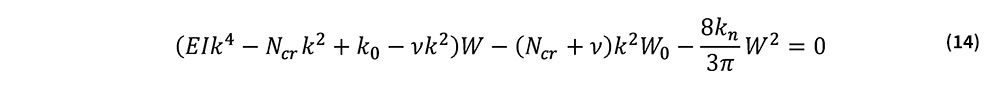
ここで,EIk4-Ncrk2+k0=0であり,またνW0≈0と近似すると次式を得る.
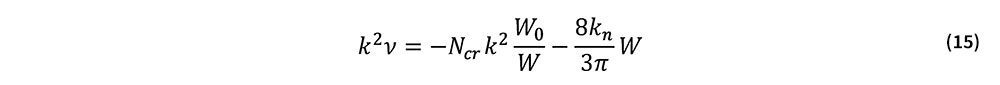
式(15)はW0≠0におけるつり合い経路を与える.飛び移り座屈は,当該経路上の極大点で発生する.そこで,式(15)の両辺をWについて微分し,dν/dW=0とおき,飛び移り座屈点におけるWを求めると次式を得る.
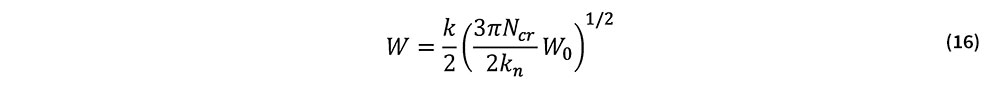
式(16)をつり合い式(15)に代入し,νについて解くと次式を得る.
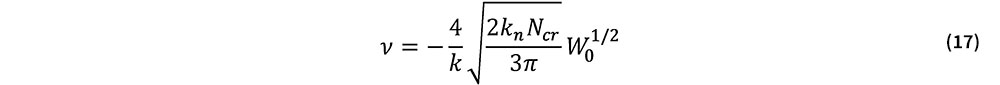
式(17)をN=Ncr+νに代入し,式(11)の最小分岐座屈軸力を与える波数kmを波数kとして用いると,次に示す飛び移り座屈時の軸力Nと初期通り変位振幅W0との関係式が得られる.
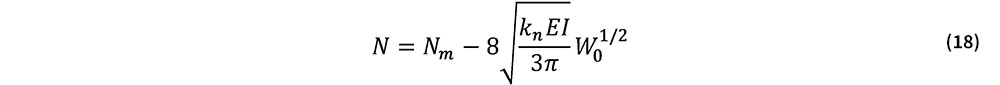
式(18)より,飛び移り座屈時の軸力は,W0の1/2乗に比例して低下することがわかる.この座屈荷重低下曲線は,図-1の右図に対応しており,僅かなW0の存在下でも座屈軸力がNmから大幅に低下することを示唆している.このような座屈特性のことを初期不整鋭敏性と呼ぶ.
また,式(18)右辺第2項目には,道床横抵抗力における非線形項knが含まれている.このことより,当該の非線形性の存在によって,軌道の座屈形態が初期不整に鋭敏な飛び移り座屈で与えられることが理解できる.なおknが正値をとる条件は,軌道横変位と道床横抵抗力との関係が上に凸な曲線で与えられる場合に対応する.よって,道床横抵抗力が式(2)に示される様な上限値g0に漸近するものでは無く,wLRと共に無限に増大する曲線で与えられる場合でも,それが上に凸である限り飛び移り座屈を生ずることがわかる.このことは軌道座屈の数値シミュレーションより容易に確認することができる.
式(11)より,分岐座屈モードは一定波長・一定振幅の波形で与えられる.しかし,実軌道で認められる座屈では,局所的に振幅が大きくなる波形が現れる.これは局所化と呼ばれる破壊現象の一つとして解釈することができる.なお,その詳細については文献[4]を参照されたい.
参考文献
- 阿部和久,水野雄太,紅露一寛 : 通り変位波形におけるバラツキが軌道座屈強度の確率特性に及ぼす影響,鉄道工学シンポジウム論文集,No.24, 167-174, 2020.
- 沼田 実 : ロング・レールの座屈強さ,鉄道技術研究報告,No.721, 1970.
- 宮井 徹 : エネルギー法による軌道座屈の数値解析,鉄道技術研究報告, No.1271, 1984.
- 阿部和久,田中洋介,西宮裕騎,紅露一寛 : レール温度座屈時の分岐過程に関する一考察,鉄道力学論文集,No.13, 7-14, 2009.